IdentifiantMot de passe
Mot de passe oublié ?Je m'inscris ! (gratuit)

FAQ mathématiques pour les jeux

FAQ mathématiques pour les jeuxConsultez toutes les FAQ

Nombre d'auteurs : 7, nombre de questions : 82, dernière mise à jour : 15 juin 2021 

 
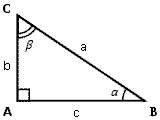
OuvrirSommaire→Trigonométrie→Triangles rectangles
précédentsommairesuivant
 Version PDF Version hors-ligne 
 
 
HautPage
Quelles sont les relations entre les longueurs et les angles d'un triangle rectangle ?

Pour référence, prenons ce triangle rectangle.

Image non disponible
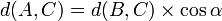
d(A,C)=d(B,C)\times\cos{\alpha}
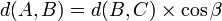
d(A,B)=d(B,C)\times\cos{\beta}
Dans un triangle rectangle, la mesure d'un côté de l'angle droit est égale au produit de la mesure de l'hypoténuse par le cosinus de l'angle compris.
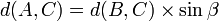
d(A,C)=d(B,C)\times\sin{\beta}
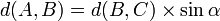
d(A,B)=d(B,C)\times\sin{\alpha}
Dans un triangle rectangle, la mesure d'un côté de l'angle droit est égale au produit de la mesure de l'hypoténuse par le sinus de l'angle opposé.
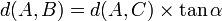
d(A,B)=d(A,C)\times\tan{\alpha}
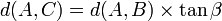
d(A,C)=d(A,B)\times\tan{\beta}
La mesure d'un côté de l'angle droit est égale au produit de la mesure de l'autre côté de l'angle droit par la tangente de l'angle opposé à ce côté.

Ces formules sont aussi parfois exprimées en fonction du nombre trigonométrique.

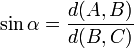
\sin{\alpha} = \frac{d(A,B)}{d(B,C)}
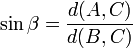
\sin{\beta} = \frac{d(A,C)}{d(B,C)}
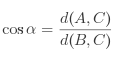
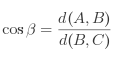
Image non disponible
Image non disponible
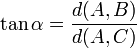
\tan{\alpha} = \frac{d(A,B)}{d(A,C)}
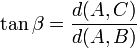
\tan{\beta} = \frac{d(A,C)}{d(A,B)}

Il ne faut pas oublier que, la somme des amplitudes des angles d'un triangle valant \pi, la somme des amplitudes des angles aigus d'un triangle vaut \frac{\pi}{2}.

De même, voici pour rappel le théorème de Pythagore.

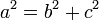
a^2 = b^2 + c^2
Créé le 16 septembre 2010  par Thibaut Cuvelier
 
HautPage
Comment résoudre un cas classique de triangle rectangle ?

Résoudre un triangle, c'est calculer ses éléments inconnus en fonction d'éléments connus.

On peut remarquer qu'il s'agit souvent de résoudre le même genre de triangles : c'est ce que l'on appelle des cas classiques. Les éléments donnés sont des angles du triangle et/ou des côtés du triangle.

Dans cette réponse, on considèrera :

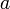  • a comme l'hypoténuse ;
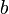  • b comme un côté de l'angle droit ;
  • c comme l'autre côté de l'angle droit ;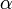
  • \alpha comme l'angle droit ;
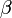  • \beta comme un angle aigu ;
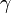  • \gamma comme l'autre angle aigu.

Premier cas : on donne l'hypoténuse a et un angle aigu \beta.
Image non disponible
Image non disponible
Image non disponible

Deuxième cas : on donne un côté de l'angle droit b et un angle aigu \beta.
Image non disponible
Image non disponible
Image non disponible

Troisième cas : on donne l'hypoténuse a et un côté de l'angle droit b.
Image non disponible
Image non disponible
Image non disponible

Quatrième cas : on donne les deux côtés de l'angle droit, b et c.
Image non disponible
Image non disponible
Image non disponible

Créé le 16 septembre 2010  par Thibaut Cuvelier
précédentsommairesuivant
 Version PDF Version hors-ligne 
 

Les sources présentées sur cette page sont libres de droits et vous pouvez les utiliser à votre convenance. Par contre, la page de présentation constitue une œuvre intellectuelle protégée par les droits d'auteur. Copyright © 2005-2014 Developpez LLC et al. Aucune reproduction, même partielle, ne peut être faite de ce site ni de l'ensemble de son contenu : textes, documents, images, etc. sans l'autorisation expresse de l'auteur. Sinon vous encourez selon la loi jusqu'à trois ans de prison et jusqu'à 300 000 € de dommages et intérêts.