FAQ mathématiques pour les jeux

FAQ mathématiques pour les jeuxConsultez toutes les FAQ
Nombre d'auteurs : 7, nombre de questions : 82, dernière mise à jour : 15 juin 2021
 Sommaire→Trigonométrie→Triangles quelconques
Sommaire→Trigonométrie→Triangles quelconquesLes côtés d'un triangle sont proportionnels aux sinus des angles opposés. Le facteur de proportionnalité est le diamètre du cercle circonscrit à ce triangle.
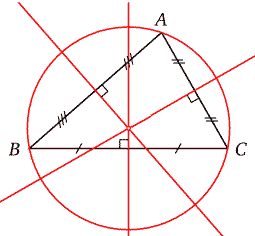
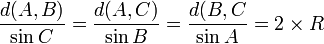
Le carré d'un côté d'un triangle est égal à la somme des carrés des deux autres côtés diminuée du double produit de ces côtés et du cosinus de l'angle qu'ils délimitent.
Pour référence, prenons ce triangle.
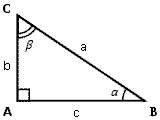
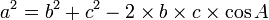
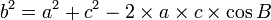
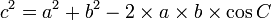
L'aire d'un triangle vaut le demi-produit de deux côtés et de l'angle formé par ces deux côtés.
Ou, le double de l'aire d'un triangle est le produit de deux côtés et de l'angle formé par ces deux côtés.
Pour référence, prenons ce triangle.

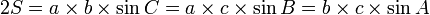
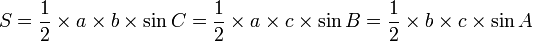
Résoudre un triangle, c'est calculer ses éléments inconnus en fonction d'éléments connus.
On peut remarquer qu'il s'agit souvent de résoudre le même genre de triangles : c'est ce que l'on appelle des cas classiques. Les éléments donnés sont des angles du triangle et/ou des côtés du triangle.
Dans cette réponse, on considèrera :
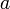 ,
, 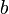 et
et  comme les trois côtés d'un triangle ;
comme les trois côtés d'un triangle ; 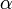 ,
, 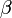 et
et 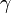 comme les trois angles du triangle.
comme les trois angles du triangle.
Premier cas : on donne les trois côtés, ![]() ,
, ![]() et
et ![]() .
.
Trois jeux de formules existent pour résoudre ce cas.
Afin de faciliter les calculs, posons : ![]()
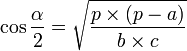
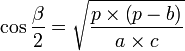
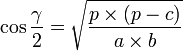
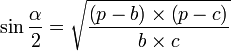
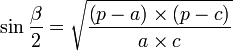
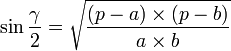
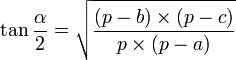
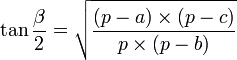
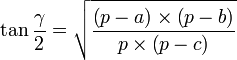
On peut aussi résumer ce cas classique d'une autre manière. On utilise uniquement le théorème d'Al-Kashi sur chacun des côtés afin de trouver les angles. Si l'on utilisait la règle des sinus par après, plusieurs solutions seraient possibles pour chaque angle, il faudrait faire une disjonction de cas.
Il faut aussi vérifier que le triangle soit possible ! Pour cela, une simple propriété : dans un triangle, la longueur de tout côté doit être inférieure à la somme des longueurs deux autres.
Deuxième cas : on donne deux côtés ainsi que l'angle compris entre ces deux côtés.
Grâce au théorème d'Al-Kashi, on peut facilement trouver la longueur du troisième côté. Le même théorème peut être employé pour les deux derniers angles.
Troisième cas : on donne un côté et les deux angles adjacents à ce côté.
Comme la somme des amplitudes des angles d'un triangle est constante, on peut facilement calculer le dernier angle. Les deux derniers côtés s'obtiennent par la règle des cosinus ou par la règle des sinus.
Quatrième cas : on donne deux côtés, ![]() et
et ![]() et l'angle opposé à l'un d'eux,
et l'angle opposé à l'un d'eux, ![]() .
.![]() . Deux valeurs de
. Deux valeurs de ![]() sont possibles :
sont possibles : ![]() et
et ![]() .
.
Le dernier angle ![]() accepte donc aussi deux valeurs :
accepte donc aussi deux valeurs : ![]() et
et ![]() .
.
Nous pouvons donc calculer le dernier côté : ![]()
![]() .
.
Plusieurs cas sont possibles avec ces données : deux triangles peuvent correspondre, tout aussi bien qu' un seul, ou bien zéro !



