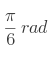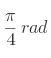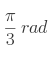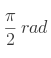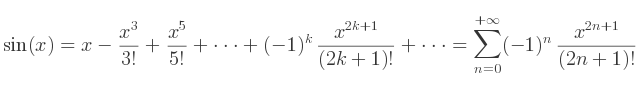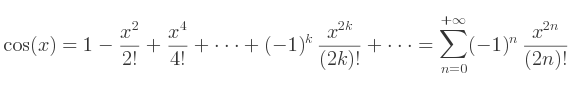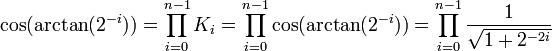FAQ mathématiques pour les jeux

FAQ mathématiques pour les jeuxConsultez toutes les FAQ
Nombre d'auteurs : 7, nombre de questions : 82, dernière mise à jour : 15 juin 2021
 Sommaire→Trigonométrie→Trigonométrie Bases
Sommaire→Trigonométrie→Trigonométrie Bases- Qu'est-ce que la trigonométrie ?
- Quelles sont les mesures de l'angle ?
- Qu'est-ce que le cercle trigonométrique ?
- Que sont les angles associés ?
- Qu'est-ce qu'un nombre trigonométrique ?
- À partir d'un nombre trigonométrique, comment calculer les autres ?
- Quels sont les nombres trigonométriques des angles remarquables ?
- Comment implémenter une fonction trigonométrique à partir des séries entières ?
- Comment implémenter une fonction trigonométrique en utilisant l'algorithme CORDIC ?
- Comment fonctionnent les look up tables ?
La trigonométrie est la branche des mathématiques qui étudie les relations entre les longueurs des côtés des triangles et leurs angles, et, par extension, les fonctions trigonométriques (sinus, cosinus et leurs dérivés : tangente, cotangente, sécante, cosécante).
La trigonométrie est très souvent utilisée dans des domaines très variés. Par exemple, elle est très utile dans l'optique (pour les microscopes, par exemple) ou la physique newtonienne (lois des mouvements…), ou pour la triangulation, qui permet de localiser un point en mesurant les angles formés avec d'autres points de référence.
Il existe deux mesures principales de l'angle : le degré et le radian. Il existe aussi le quadrant, la mesure d'angle d'un angle droit. Un cercle décrit un angle de 360°, de 4q et de ![]() .
.
° est le symbole du degré, q celui du quadrant, et rad celui du radian.
Un radian est la mesure de l'angle dont la mesure de l'arc interceptant un cercle vaut le rayon de ce cercle.
Un quadrant est le quart de l'angle formé par un cercle.
Un degré est le 360e de l'angle formé par un cercle.
Ceci permet d'écrire les égalités suivantes :
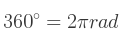
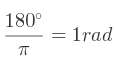

Ces égalités permettent de facilement convertir une mesure d'angle des degrés en radians et inversement. Voici de telles fonctions avec leurs notations mathématiques.
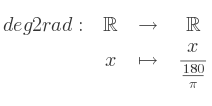
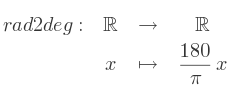
Et voici son implémentation en C99, compatible C++.
#define PI 3.141592653589793
inline
long double deg2rad (float deg)
{
return deg / (180 / PI);
}
inline
long double rad2deg (float rad)
{
return rad * (180 / PI);
}Il existe encore d'autres mesures d'angle, mais elles sont nettement moins utilisées : le grade, le mil, la révolution (ou rotation), le degré binaire, le radian binaire (bradian), l'angle horaire, le gradient…
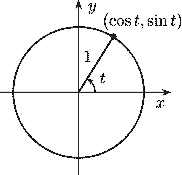
Le cercle trigonométrique est le cercle dont le centre est le centre du repère et de rayon 1. C'est pourquoi il est aussi appelé cercle unité : chacun de ses points se situe à une unité du centre du repère. Ces points ont des abscisses et des ordonnées un peu particulières : elles correspondent au sinus et au cosinus de l'angle orienté formé par l'axe des abscisses et la droite passant par ce point et le centre du repère.
Voici les équations paramétriques de ce cercle :
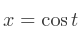
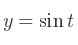
On utilise généralement le sens trigonométrique pour parcourir ce cercle : il est opposé au sens horloger. On parle aussi exceptionnellement du sens senestre (par opposition à dextre).
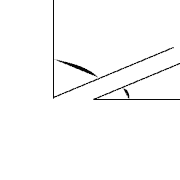 Deux angles sont complémentaires si la somme de leurs mesures d'angle équivaut la mesure d'un angle droit.
Deux angles sont complémentaires si la somme de leurs mesures d'angle équivaut la mesure d'un angle droit.
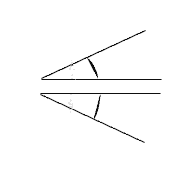 Deux angles sont opposés si leurs mesures d'angle sont opposées.
Deux angles sont opposés si leurs mesures d'angle sont opposées.
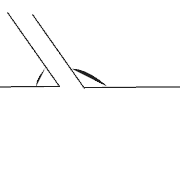 Deux angles sont supplémentaires si la somme de leurs mesures d'angle équivaut la mesure d'un angle plat.
Deux angles sont supplémentaires si la somme de leurs mesures d'angle équivaut la mesure d'un angle plat.
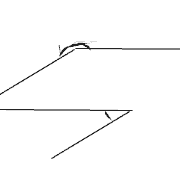 Deux angles sont antisupplémentaires si l'un équivaut l'autre à la mesure d'un angle plat près.
Deux angles sont antisupplémentaires si l'un équivaut l'autre à la mesure d'un angle plat près.
En effet, lors d'un travail en radians,
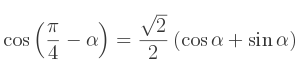
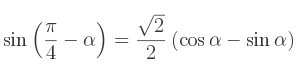
De même,
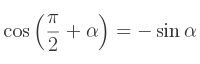
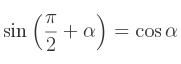
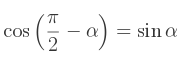
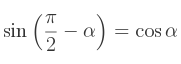
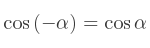
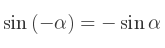
Un nombre trigonométrique est le résultat d'une fonction trigonométrique (sinus, cosinus, tangente, cotangente…). Par exemple :
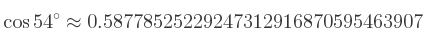
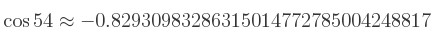
Un nombre trigonométrique peut être calculé assez exactement par une machine, ou bien être approché grâce au cercle trigonométrique.
Dans la figure suivante, on a tracé un angle. Pour en trouver le sinus, il suffit de tracer la parallèle à l'axe des cosinus passant par le point de contact entre la demi-droite bornant l'angle et le cercle trigonométrique et de mesurer la distance entre l'axe des cosinus et cette droite.
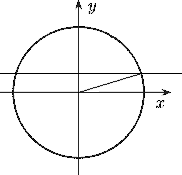
Il faut plusieurs relations entre les différents nombres trigonométriques afin de pouvoir les exprimer les uns par rapport aux autres.
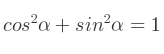
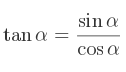
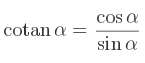
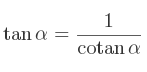
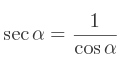
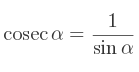
Avec ces quelques relations, vous pouvez sans problème trouver tous les nombres trigonométriques de l'angle dont vous avez un nombre trigonométrique.
La relation fondamentale exprimée en fonction du cosinus pour obtenir facilement le sinus :
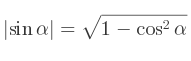
La relation fondamentale exprimée en fonction du sinus pour obtenir facilement le cosinus :
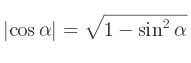
La définition de la tangente en fonction du cosinus :
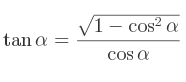
La définition de la cotangente en fonction du sinus :
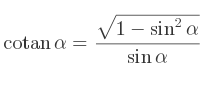
Premièrement, quels sont les angles remarquables ?
En degrés : 0°, 30°, 45°, 60°, 90°.
En radians : ![]() ,
, 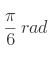 ,
, 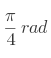 ,
, 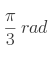 ,
, 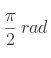 .
.
Qu'ont-ils de particulier ? Il est possible de démontrer leurs cosinus et sinus, pour obtenir une fraction (ir)rationnelle assez simple.
|
|
|
|
|
|
|
|---|---|---|---|---|---|
|
Sinus |
|
|
|
|
|
|
Cosinus |
|
|
|
|
|
Une des manières les plus simples est d'utiliser les séries entières. Les voici.
Plus on développe la série, plus le résultat devient précis, mais lent à calculer.
Voici une implémentation du calcul du sinus par cette méthode en C99, compatible C++.
Et voici son pendant pour le cosinus par cette méthode en C99, compatible C++.
Ces implémentations ne sont pas prévues pour être rapides, il s'agit juste de montrer comment faire. Un certain nombre d'optimisations peuvent être envisagées.
Cet algorithme recherche les coordonnées de l'intersection de l'angle avec le cercle trigonométrique. Il procède avec un vecteur ![]() , qu'il fait tourner pour qu'il atteigne l'angle recherché.
, qu'il fait tourner pour qu'il atteigne l'angle recherché.
À chaque itération, on calcule la multiplication du vecteur ![]() avec une matrice de transformation,
avec une matrice de transformation, ![]()
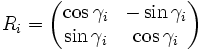
En mettant le facteur ![]() en évidence, on obtient :
en évidence, on obtient :
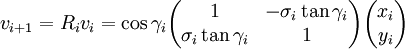
Le facteur ![]() peut valoir -1 ou +1 en fonction du sens de rotation. Si on restreint les valeurs de
peut valoir -1 ou +1 en fonction du sens de rotation. Si on restreint les valeurs de ![]() afin que
afin que ![]() soit égal à
soit égal à ![]() , alors la multiplication par le facteur tangente devient une multiplication par une puissance de 2. D'où :
, alors la multiplication par le facteur tangente devient une multiplication par une puissance de 2. D'où :
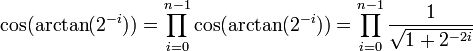
Le facteur ![]() peut être ignoré pendant l'itération, et factorisé en un seul coefficient multiplicatif final. Ici, n représente le nombre d'itérations.
peut être ignoré pendant l'itération, et factorisé en un seul coefficient multiplicatif final. Ici, n représente le nombre d'itérations.
La limite de ce produit lorsque n tend vers l'infini est de 0,607 252 94.
Après suffisamment d'itérations, l'angle formé par le vecteur et l'axe des cosinus se rapprochera de l'angle dont on recherche les sinus et cosinus.
La dernière étape consiste à déterminer à chaque itération le sens de rotation : trigonométrique (antihoraire) ou horaire. Ce résultat influence la valeur de ![]() .
.
Tout simplement, on soustrait la mesure de l'angle ![]() à la mesure de l'angle désiré. Si le résultat est positif, on tourne dans le sens horloger. S'il est négatif, on tourne dans le sens trigonométrique. Cette étape peut être déclarée dichotomique.
à la mesure de l'angle désiré. Si le résultat est positif, on tourne dans le sens horloger. S'il est négatif, on tourne dans le sens trigonométrique. Cette étape peut être déclarée dichotomique.
![]()
![]()
Voici maintenant l'implémentation de cet algorithme en C99, compatible C++.
Une look up table (ou LUT) est un tableau statique à chargement dynamique. Dit autrement, il s'agit d'une sorte de tableau qui est construit dynamiquement (typiquement au lancement du programme, quand il affiche son splash screen) dont l'accès aux données se fait comme s'il était stocké dans le binaire.
Une LUT sert principalement à accélérer le calcul de valeurs de fonctions prenant un certain temps à calculer, surtout quand on en a besoin très souvent (par exemple, une application devant calculer des milliers de cosinus par seconde pourra en profiter, ils seront déjà calculés, il suffira d'aller les lire).
Son fonctionnement est très simple : il s'agit tout d'abord d'un conteneur un peu spécial. Il stocke des valeurs d'une fonction pour un paramètre précis, ce paramètre servant d'indice au tableau (pour l'implémentation, on utilise généralement un vecteur). Seulement, ces indices sont forcément entiers alors que les paramètres, surtout en trigonométrie, ne sont que très rarement entiers. Il faut donc un peu tricher à cet endroit pour transformer ces flottants en entiers (un exemple est disponible ci-dessous).
#include <vector>
#include <cmath>
using namespace std;
class lut
{
private:
vector<float> m_lut;
float m_min;
float m_max;
float m_precision;
public:
lut() {}
~lut() {}
// L'intervalle dans lequel on devra calculer les valeurs prises par la fonction
void setInterval (float min, float max)
{
this->m_min = min;
this->m_max = max;
}
// Donne la précision, la différence entre les paramètres de deux valeurs stockées
void setPrecision (float p)
{
this->m_precision = p;
}
// Calcule les valeurs demandées
void compute()
{
for(float x = this->m_min, int i = 0 ; x <= this->m_max ; x += this->m_precision, ++i)
{
this->m_lut[i] = cos(x);
}
// Le code est assez clair : pour toutes les valeurs entre this->m_min et this->m_max,
// on calcule le cosinus de cette valeur et on l'inscrit dans la LUT.
// Seulement, un vecteur n'aime pas trop les float comme indices, il faut donc tricher :
// 0 -> this->m_min
// 1 -> this->m_mix + this->m_precision
// etc.
// Problème : il faut retransformer les valeurs demandées en indices du vecteur.
// Cependant, cela évite de créer son propre conteneur, ce qui n'est pas le but ici.
// Ce code est loin d'être optimal, il ne donne qu'une manière de faire, qui ne veut pas
// être la meilleure, mais juste suffisamment simple à comprendre.
}
float get(float x)
{
// On veut forcément une valeur dans l'intervalle ; sinon, cette implémentation calcule cette valeur précise, mais ne la stocke pas.
if ( ! (x > this->m_min && x < this->m_max) )
return cos(x);
// La valeur 0 correspond au minimum : si x vaut ce minimum, il doit valoir 0, on ne peut pas le créer autrement.
x -= this->m_min;
// Toutes les valeurs ne sont pas disponibles : on divise donc par la précision pour avoir une valeur comme ce que nous voulons.
x /= this->m_precision;
// x est toujours un flottant, on veut un entier : il suffit de perdre les décimales pour obtenir notre indice !
int i = floor(x); // vous auriez pu utiliser ceil ou une autre méthode pour récupérer un entier
// Maintenant, on retourne à l'utilisateur le résultat demandé.
return this->m_lut[i];
}
};Cette implémentation d'une LUT n'est pas forcément la meilleure possible ! Il ne s'agit que d'un exemple pour vous aider à comprendre leur principe ; en réalité, vous devriez plutôt prévoir une LUT plus réutilisable (notamment pas autant liée à une fonction, ne pas mettre en dur la fonction dont vous calculez les images), plus optimisée en fonction de vos besoins (vos indices seront peut-être exclusivement entiers, un pan entier de cette implémentation peut ainsi être évité).
lut m_lut;
m_lut->setInterval(0, 1.57); // de 0 à PI/2
m_lut->setPrecision(0.157); // soit PI/20
m_lut->compute();
cout << m_lut->get(0.157); // récupérée de la lut, valeur déjà calculée
cout << m_lut->get(0.158); // valeur en dehors de la lut, calculée à ce moment-làCet exemple de LUT peut être fortement amélioré : on pourrait, par exemple, instaurer un système d'interpolation pour les valeurs pour lesquelles rien n'est calculé. Il serait possible de coder son propre conteneur à cet effet et d'autoriser alors l'utilisation d'indices flottants, par exemple ce qui est disponible avec les tableaux CUDA normalisés (ils n'autorisent que des indices entre 0 et 1).
Utiliser une LUT n'a de sens que si vous devez obtenir très souvent le résultat d'une fonction ! S'il s'agit simplement de calculer trois cosinus sur toute la durée de vie de l'application, elle perdra beaucoup de temps à créer cette LUT et prendra beaucoup de mémoire pour la stocker pour rien. Il n'est pas non plus intéressant d'utiliser une LUT pour des opérations très simples, l'accès à un élément ayant un coût non négligeable pour ce genre d'opérations.