FAQ mathématiques pour les jeux

FAQ mathématiques pour les jeuxConsultez toutes les FAQ
Nombre d'auteurs : 7, nombre de questions : 82, dernière mise à jour : 15 juin 2021
 Sommaire→Quaternions
Sommaire→Quaternions- Qu'est-ce que les quaternions ?
- Quel est le rapport entre les quaternions et l'animation 3D ?
- Comment calculer le conjugué d'un quaternion ?
- Comment calculer la norme d'un quaternion ?
- Comment normaliser un quaternion ?
- Comment calculer l'inverse d'un quaternion ?
- Comment multiplier deux quaternions ?
- Comment convertir un quaternion en matrice de rotation ?
- Comment convertir une matrice de rotation en un quaternion ?
- Comment convertir un axe de rotation et un angle en un quaternion ?
- Comment convertir un quaternion en un axe de rotation et un angle ?
- Comment convertir des angles de rotations sphériques en un quaternion ?
- Comment convertir un quaternion en des angles de rotations sphériques ?
- Comment convertir des angles d'Euler en un quaternion ?
- Comment utiliser des quaternions pour réaliser une interpolation linéaire entre matrices ?
Les quaternions permettent d'étendre la notion de rotation en 3 dimensions à celle en 4 dimensions. Ils permettent ainsi
- d'éviter le gimbal lock et
- l'implémentation de rotations plus continues et plus précises.
Un quaternion est défini via l'usage de 4 valeurs réelles (x, y, z, w).
Elles sont calculées par une combinaison des 3 coordonnées de l'axe de rotation et de l'angle correspondant.
Comme mentionné plus haut, les angles d'Euler ont quelques défauts dus à l'ordre dans lequel sont réalisées les rotations.
Les quaternions résolvent ce problème. Au lieu de tourner un objet via une série de rotations successives, les quaternions permettent au programmeur de tourner un objet autour d'un axe arbitraire et d'un angle quelconque.
La rotation est néanmoins toujours réalisée par des calculs matriciels. Néanmoins, au lieu de multiplier les matrices ensemble, les quaternions les représentant sont multipliés. Le résultat final est reconverti en la matrice désirée.
Les quaternions offrent aussi l'avantage de permettre l'interpolation. Ceci permet des rotations plus souples et plus réalistes.
Ceci peut être fait en inversant le signe de la partie vectorielle du quaternion :

quaternion_conjugate(QUAT *qr, QUAT *qa)
{
qr->qw = qa->qw;
qr->qx = -qa->qx;
qr->qy = -qa->qy;
qr->qz = -qa->qz;
}La norme se calcule en multipliant le quaternion par son conjugué.
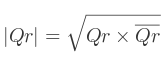
Ce qui peut s'implémenter comme suit :
QFLOAT quaternion_magnitude(QUAT *qa)
{
return sqrt(qa->qw * qa->qw +
qa->qx * qa->qx + qa->qy * qa->qy + qa->qz * qa->qz);
}Un quaternion non nul peut se normaliser de la même manière qu'un vecteur non nul : on le divise par sa norme.
Un quaternion dont la norme vaut 1 est appelé quaternion unitaire.
Calculer l'inverse d'un quaternion revient à calculer son conjugué, dans le cas où celui-ci est normalisé.
S'il n'est pas normalisé, on calcule l'inverse de cette manière :
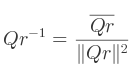
Soit deux quaternions Q1 et Q2, l'objectif est de calculer la rotation combinée Qr :
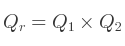
Ceci peut se faire via cette expression :
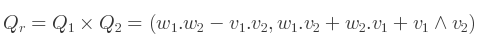
Où :
v1 = (x,y,z) de Q1
w1 = (w) de Q1
v2 = (x,y,z) de Q2
w2 = (w) de Q2Ceci peut s'implémenter comme suit :
quaternion_multiply(QUAT *qr, QUAT *qa, QUAT *qb)
{
qr.scalar = v3_dot(&qa->vector, &qb->vector);
v3_cross(&va, &qa->vector, &qb->vector);
v3_scalef(&vb, &qa->vector, &qb->scalar);
v3_scalef(&vc, &qb->vector, &qa->scalar);
v3_add(&va, &va, &vb);
v3_add(&qr->vector, &va, &vc);
quaternion_normalise(qr);
}Soit un quaternion Q :
Q = (X, Y, Z, W)Alors, ce quaternion peut se convertir en une matrice de rotation 3x3 comme suit :
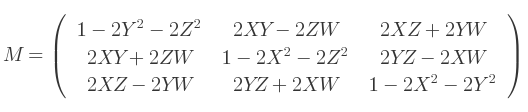
Si une matrice 4x4 est requise, alors la dernière ligne et la dernière colonne peuvent être mises à 0, et M3, 3 à 1.
La matrice peut se générer via ces expressions :
xx = X * X;
xy = X * Y;
xz = X * Z;
xw = X * W;
yy = Y * Y;
yz = Y * Z;
yw = Y * W;
zz = Z * Z;
zw = Z * W;
mat[0] = 1 - 2 * ( yy + zz );
mat[1] = 2 * ( xy - zw );
mat[2] = 2 * ( xz + yw );
mat[4] = 2 * ( xy + zw );
mat[5] = 1 - 2 * ( xx + zz );
mat[6] = 2 * ( yz - xw );
mat[8] = 2 * ( xz - yw );
mat[9] = 2 * ( yz + xw );
mat[10] = 1 - 2 * ( xx + yy );
mat[3] = mat[7] = mat[11] = mat[12] = mat[13] = mat[14] = 0;
mat[15] = 1;Une matrice de rotation peut se convertir à l'aide de l'algorithme suivant.
On commence par calculer la trace de la matrice, c'est-à-dire la somme de ses éléments diagonaux :
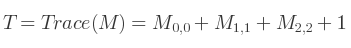
Si la trace est positive, alors le calcul est instantané :
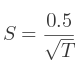
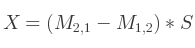
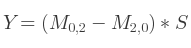
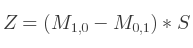
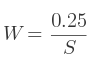
Si par contre la trace de la matrice est égale à 0, alors il faut identifier l'élément le plus grand dans la diagonale principale de la matrice.
En fonction de la position de cette valeur :
Si c'est M0, 0 :
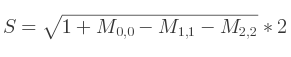
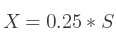
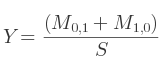
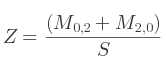
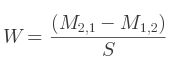
Si c'est M1, 1 :
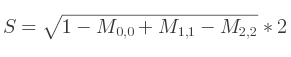
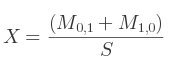
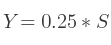
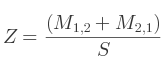
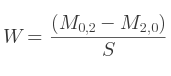
Si c'est M2, 2 :
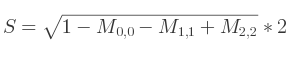
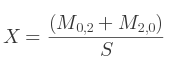
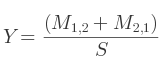
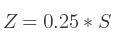
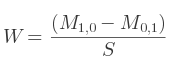
Le quaternion est finalement défini par Q = (X, Y, Z, W).
Étant donné l'axe de rotation et l'angle, cet algorithme peut être utilisé pour générer un quaternion :
sin_a = sin(angle / 2)
cos_a = cos(angle / 2)
q->x = axis->x * sin_a
q->y = axis->y * sin_a
q->z = axis->z * sin_a
q->w = cos_a
quaternion_normalise(q);Il est nécessaire de normaliser le quaternion par la suite.
Un quaternion peut se reconvertir en un angle et un axe de rotation très facilement, sachant que w est le cosinus du demi-angle, et que (x, y, z) représente l'axe de rotation :
/* Normalisation du quaternion */
quaternion_normalise(qr);
/* Récupération de l'angle de rotation */
angle = acos(qr->qw) * 2;
/* Récupération des composantes de l'axe de rotation */
vx = qr->qx;
vy = qr->qy;
vz = qr->qz;
/* Normalisation de l'axe de rotation */
norm = sqrt(vx * vx + vy * vy + vz * vz);
if (norm > 0.0005)
{
vx /= norm;
vy /= norm;
vz /= norm;
}Un axe de rotation peut être défini par des coordonnées sphériques (latitude et longitude) et un angle de rotation.
Dans ce cas, le quaternion peut être calculé comme suit :
sin_a = sin(angle / 2)
cos_a = cos(angle / 2)
sin_lat = sin(latitude)
cos_lat = cos(latitude)
sin_long = sin(longitude)
cos_long = cos(longitude)
qx = sin_a * cos_lat * sin_long
qy = sin_a * sin_lat
qz = sin_a * sin_lat * cos_long
qw = cos_aUn quaternion peut se convertir en coordonnées sphériques via :
/* Récupération de l'angle de rotation */
angle = acos(q->qw) * 2;
/* Récupération des composantes de l'axe de rotation */
vx = qr->qx;
vy = qr->qy;
vz = qr->qz;
/* Normalisation de l'axe de rotation */
norm = sqrt(vx * vx + vy * vy + vz * vz);
if (norm > 0.0005)
{
vx /= norm;
vy /= norm;
vz /= norm;
}
/* Calcul de la latitude */
latitude = -asin(vy);
/* Calcul de la longitude */
if (vx * vx + vz * vz < 0.0005)
longitude = 0;
else
longitude = atan2(vx, vz);
/* Si la longitude est négative, on la ramène du côté positif */
if (longitude < 0)
longitude += 2 * PI;La conversion d'angles d'Euler en quaternion peut se faire à l'aide de multiplication de quaternions. Chaque angle de rotation est converti en une paire angle-axe, chaque axe correspondant à un axe euclidien. Ces paires sont converties en quaternions qui sont multipliés ensemble.
Implémentation :
quaternion_from_euler(QUATERNION *q, VFLOAT ax, VFLOAT ay, VFLOAT az)
{
VECTOR3 vx = {1, 0, 0}, vy = {0, 1, 0}, vz = {0, 0, 1};
QUATERNION qx, qy, qz, qt;
quaternion_from_axisangle(qx, &vx, ax);
quaternion_from_axisangle(qy, &vy, ay);
quaternion_from_axisangle(qz, &vz, az);
quaternion_multiply(&qt, &qx, &qy);
quaternion_multiply(q, &qt, &qz);
}Dans beaucoup d'applications, il peut être nécessaire d'interpoler entre deux positions de rotation d'un objet donné. Ces positions peuvent être spécifiées à l'aide de l'animation par keyframe ou cinématique inverse.
Il est nécessaire d'avoir au moins deux matrices, la matrice de départ et la matrice finale (MS et MF).
En interpolation linéaire, la matrice de rotation interpolée est générée en utilisant une équation paramétrique où t varie de 0.0 à 1.0.
À t = 0, la matrice interpolée est égale à la matrice de départ. À t = 1, la matrice interpolée est égale à la matrice de fin.
Donc, la matrice de rotation interpolée (MI) est spécifiée par :
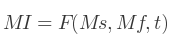
Où F est une fonction d'interpolation.
La première étape est de calculer la matrice de rotation qui va convertir MS vers MF :
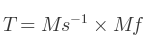
Où :
Ms est la matrice de départ,
Mf est la matrice finale,
et T la matrice intermédiaire.
Ensuite, il convient de convertir cette matrice en un axe et un angle de rotation à l'aide des quaternions.
Afin de générer la matrice de rotation désirée, il suffit de modifier l'angle de rotation en fonction de t et de reconstruire la matrice de rotation voulue.
Exemple :
m4_transpose(mt, ms); /* Inversion */
m4_mult(ms, mt, mb); /* Matrice de Rotation */
m4_to_axisangle(ms, axis, angle); /* Rotation axe/angle */for (t = 0; t < 1.0; t += 0.05)
{
m4_from_axisangle(mi, axis, angle * t); /* Interpolation Finale */
/* ... ce que vous voulez ... */
}où t est le facteur d'interpolation allant de 0.0 à 1.0.



