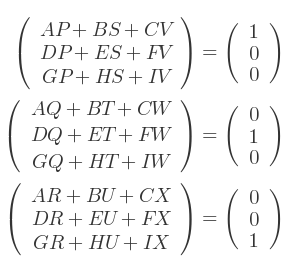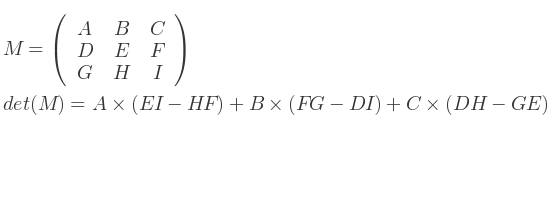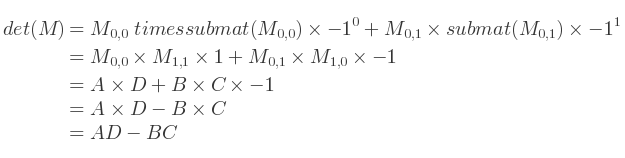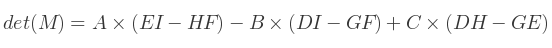Le déterminant d'une matrice est un réel qui permet entre autres de savoir si la matrice admet ou non un inverse. S'il est nul, aucun inverse n'existe. Le déterminant n'est calculable que sur les matrices carrées (possédant autant de lignes que de colonnes).

Par exemple, soit la matrice à un seul élément :

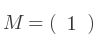
Pour une matrice de cette taille, le déterminant est simplement la valeur de l'élément.

Du coup, l'inverse est simplement l'inverse de cet élément :

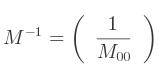
Si cette valeur est non nulle, l'inverse existe. Dans le cas de la matrice identité, l'inverse est la matrice identité.

Néanmoins, si la valeur de l'élément est nulle, le déterminant est nul également.

Essayer de calculer la réciproque de zéro génère l'infini, ce qui entraine que cette matrice n'a pas d'inverse.

Pour la matrice identité, le déterminant est toujours 1. Toute matrice avec un déterminant égal à 1 est dite isotropique.

Ainsi, toutes les matrices de rotations sont dites isotropiques, puisque leur déterminant est toujours égal à 1.

Par exemple, soit M une matrice de rotation :

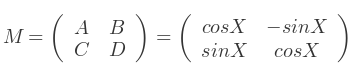
Voici le calcul de son déterminant :

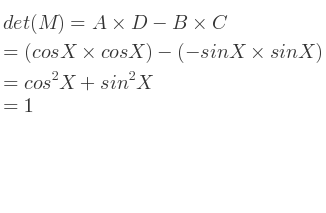
Le déterminant d'une matrice se calcule à l'aide des règles de Kramer, qui permet de le calculer en découpant la matrice en des matrices plus petites.

La formule est la suivante, pour une matrice carrée M de dimension n :

où définit la matrice composée de toutes les lignes et de toutes les colonnes de M à l'exception de la ligne i et de la colonne j.

Pour les petites matrices, la formule est immédiate. Par exemple pour les matrices 2x2 :

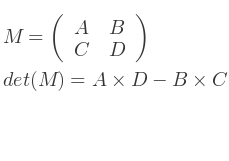
Et pour les matrices 3x3 :

Une matrice isotrope est une matrice pour laquelle les sommes des carrés des lignes ou colonnes sont égales.

Une matrice qui n'est pas dans ce cas est dite anisotrope.

Quand une matrice 3x3 ou 4x4 est utilisée pour tourner ou mettre à l'échelle un objet, il est parfois nécessaire d'agrandir ou de rétrécir un axe plus qu'un autre.

Par exemple, ça peut être utile de vouloir déformer un personnage de type cartoon vers un axe, mais pas dans les autres…

Voici une matrice de ce type :

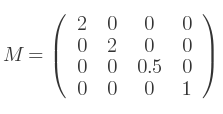
Néanmoins, bien que ce type de matrice s'applique bien pour les vertex, il se peut très bien qu'il y ait des problèmes avec les normales, en particulier en ombrage de Gouraud.

En effet, les données vertex et les normales sont multipliées par la même matrice, ce qui déforme les normales. N'étant plus normalisées, elles peuvent perturber d'autres calculs comme l'ombrage (shading) ou l'élimination des parties cachées (back-face culling).

Étant donné une matrice M, l'inverse de cette matrice, noté M^-1, est la matrice qui vérifie cette expression :

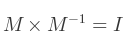
Où I est la matrice identité.

Ainsi, multiplier une matrice par son inverse génère la matrice identité. Néanmoins, plusieurs conditions doivent être réunies pour pouvoir calculer l'inverse d'une matrice.

Celles-ci incluent que la hauteur et la largeur de la matrice soient identiques, et que le déterminant de la matrice soit non nul.

L'inversion d'une matrice est une tâche souvent réalisée, par exemple pour retrouver l'inverse d'une transformation quelconque.

En fonction de la taille de la matrice, le calcul de son inverse peut être trivial ou extrêmement compliqué.

Par exemple, l'inverse d'une matrice 1x1 est juste la réciproque de l'élément :

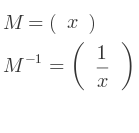
La résolution pour les matrices 2x2 ou plus peut être réalisée à l'aide de Kramer ou via un ensemble d'équations.

Néanmoins, dans certains cas comme les matrices identités ou de rotations, l'inverse est déjà connu ou peut être déterminé à l'aide de la transposée de la matrice.

L'inverse d'une matrice identité est la matrice identité :

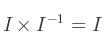
La matrice identité a pour déterminant la valeur 1.

Voici la forme générale de l'inverse d'une matrice de rotation 3x3 :

À noter que s'il s'agit d'une matrice de rotation autour de X, Y ou Z, inverser la matrice revient à calculer sa transposée.

Il existe également une autre façon de faire, si l'angle et l'axe de rotation sont connus. Il suffit de prendre l'opposé de l'angle (-20 pour 20 par exemple) et de calculer une nouvelle matrice de rotation (voir https://jeux.developpez.com/faq/math/?page=transformations#Q38).

Il faut commencer par calculer le déterminant de la matrice (voir https://jeux.developpez.com/faq/math/?page=determinants_inverses#Q15).

Si le déterminant est non nul, l'inverse de la matrice existe. Dans ce cas, la valeur de chaque élément de l'inverse est :

Cette formule est déduite de la formulation générale de l'inverse en fonction du déterminant :

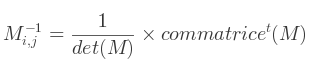
Avec la commatrice de M définie par :

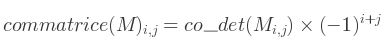
Le codéterminant (co_det) de l'élément i,j de la matrice M, est le déterminant de la matrice M dont on supprime la ligne i et la colonne j. Cette série de n² sous-matrices sont celles nommées submat(M) dans les formules précédentes.

Bien que pratique pour comprendre comment est construit l'inverse d'une matrice, elle est cependant à éviter dans un programme car nécessitant des calculs énormément coûteux au niveau du déterminant.

L'inversion et le calcul de déterminant peuvent donc en général être effectués de manière beaucoup plus efficace, par exemple en utilisant une triangularisation ou une décomposition L.U.

Pour une matrice 2x2, les calculs sont moins complexes. Soit :

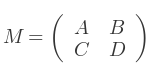
Le déterminant est :

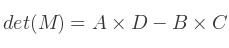
Et l'inverse se définit par :

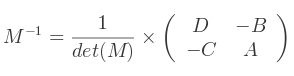
Ceci peut être démontré par les règles de Kramer. Soit :

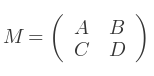
Alors, le déterminant est :

Et l'inverse s'obtient par :

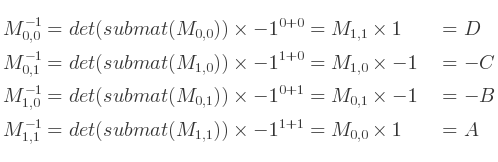
Donc l'inverse de la matrice est :

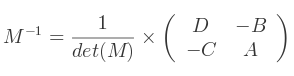
Si le déterminant est non nul.

Pour les matrices 3x3 ou plus, l'inverse peut être calculée soit à l'aide de Kramer, soit par la résolution d'un ensemble d'équations linéaires.

Si on applique les règles de Kramer à la matrice M :

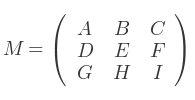
Alors, le déterminant se calcule comme suit :

En supposant que ce déterminant est non nul, alors, l'inverse de la matrice est donné par :

Ceci peut s'implémenter à l'aide d'une paire de fonctions 'C' :

VFLOAT m3_det(MATRIX3 mat)
{
    VFLOAT det;

    det = mat[0] * (mat[4] * mat[8] - mat[7] * mat[5])
        - mat[1] * (mat[3] * mat[8] - mat[6] * mat[5])
        + mat[2] * (mat[3] * mat[7] - mat[6] * mat[4]);

    return det;
}


void m3_inverse(MATRIX3 mr, MATRIX3 ma)
{
    VFLOAT det = m3_det(ma);

    if (fabs(det) < 0.0005)
    {
        m3_identity(ma);
        return;
    }

    mr[0] =   ma[4] * ma[8] - ma[5] * ma[7]  / det;
    mr[1] = -(ma[1] * ma[8] - ma[7] * ma[2]) / det;
    mr[2] =   ma[1] * ma[5] - ma[4] * ma[2]  / det;

    mr[3] = -(ma[3] * ma[8] - ma[5] * ma[6]) / det;
    mr[4] =   ma[0] * ma[8] - ma[6] * ma[2]  / det;
    mr[5] = -(ma[0] * ma[5] - ma[3] * ma[2]) / det;

    mr[6] =   ma[3] * ma[7] - ma[6] * ma[4]  / det;
    mr[7] = -(ma[0] * ma[7] - ma[6] * ma[1]) / det;
    mr[8] =   ma[0] * ma[4] - ma[1] * ma[3]  / det;
}

Les mêmes méthodes peuvent être appliquées aux matrices 3x3 et aux matrices 4x4.

Un moyen efficace est de réutiliser les fonctions 'C' utilisées pour calculer le déterminant et l'inverse d'une matrice 3x3.

Pour pouvoir utiliser les règles de Kramer, il est nécessaire de déterminer les sous-matrices :

void m4_submat(MATRIX4 mr, MATRIX3 mb, int i, int j)
{
    int ti, tj, idst, jdst;

    /* Parcours des lignes */
    for (ti = 0; ti < 4; ti++)
    {
        /* Si la ligne courante est inférieure à celle que l'on veut supprimer
           on garde l'indice tel quel */
        if (ti < i)
            idst = ti;
        else
            /* Si la ligne courante est supérieure à celle que l'on veut supprimer
               on prend l'indice - 1 */
            if (ti > i)
                idst = ti - 1;
        /* Et bien sûr si on se trouve sur la ligne à supprimer, on ne fait rien */

        /* Même traitement avec les colonnes... */
        for (tj = 0; tj < 4; tj++)
        {
            if (tj < j)
                jdst = tj;
            else
                if ( tj > j )
                    jdst = tj - 1;

            /* Si on ne se trouve pas sur la ligne ou la colonne à supprimer,
               on recopie l'élément courant dans la sous-matrice, avec le bon indice */
            if (ti != i && tj != j)
            mb[idst * 3 + jdst] = mr[ti * 4 + tj];
        }
    }
}

Le déterminant d'une matrice 4x4 peut être calculé comme suit :

VFLOAT m4_det( MATRIX4 mr )
{
    VFLOAT  det, result = 0, i = 1;
    MATRIX3 msub3;
    int     n;

    /* Parcours des colonnes */
    for (n = 0; n < 4; n++, i *= -1)
    {
        /* Extraction de la sous-matrice obtenue en retirant la colonne n */
        m4_submat(mr, msub3, 0, n);

        /* Calcul du déterminant de la sous-matrice */
        det     = m3_det(msub3);

        /* Ajout au résultat selon la formule du déterminant */
        result += mr[n] * det * i;
    }

    return result;
}

Et l'inverse :

int m4_inverse(MATRIX4 mr, MATRIX4 ma)
{
    VFLOAT  mdet = m4_det(ma);
    MATRIX3 mtemp;
    int     i, j, sign;

    /* Si le déterminant est nul, on ne peut pas inverser la matrice */
    if (fabs(mdet) < 0.0005)
        return 0;

    for (i = 0; i < 4; i++)
        for (j = 0; j < 4; j++)
        {
            sign = 1 - ((i + j) % 2 ) * 2;

            m4_submat(ma, mtemp, i, j);

            mr[i + j * 4] = (m3_det(mtemp) * sign) / mdet;
        }

    return 1;
}

Ces fonctions sont d'une utilité incroyable. Elles permettent le calcul de la matrice de base pour les splines, les rotations inverses et la résolution d'équations matricielles.

Soit M :

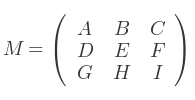
telle que l'inverse existe :

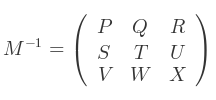
Alors on a :

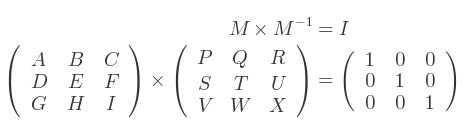
Donc, la matrice inverse peut être calculée par la résolution d'un ensemble d'équations linéaires :