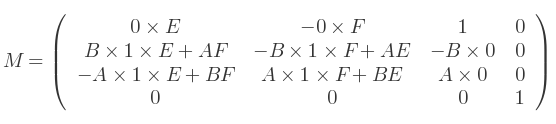FAQ mathématiques pour les jeux

FAQ mathématiques pour les jeuxConsultez toutes les FAQ
Nombre d'auteurs : 7, nombre de questions : 82, dernière mise à jour : 15 juin 2021
 Sommaire→Matrices→Transformations
Sommaire→Matrices→Transformations- Qu'est-ce qu'une matrice de rotation ?
- Comment générer une matrice de rotation d'axe X ?
- Comment générer une matrice de rotation d'axe Y ?
- Comment générer une matrice de rotation d'axe Z ?
- Qu'est-ce que les angles d'Euler ?
- Qu'est-ce que le lacet (yaw), le roulis (roll) et le tangage (pitch) ?
- Comment combiner les matrices de rotations ?
- Qu'est-ce que le gimbal lock ?
- Comment régler le problème du gimbal lock ?
- Quelle est la manière correcte de combiner les matrices de rotations ?
- Comment générer une matrice de rotation à partir d'angles d'Euler ?
- Comment générer des angles d'Euler à partir d'une matrice de rotation ?
- Comment générer une matrice de rotation pour un axe et un angle donnés ?
- Comment générer une matrice de rotation pour rendre deux vecteurs colinéaires ?
- Comment utiliser les matrices pour convertir entre deux systèmes de coordonnées ?
- Qu'est-ce qu'une matrice de translation ?
- Qu'est-ce qu'une matrice de mise à l'échelle ?
- Qu'est-ce que qu'une matrice de déformation ?
- Comment réaliser une interpolation linéaire entre deux matrices ?
- Comment réaliser une interpolation cubique entre quatre matrices ?
Une matrice de rotation est utilisée pour tourner un ensemble de points dans un système de coordonnées. Chaque point a de nouvelles coordonnées, mais leur distance relative reste inchangée.
Toutes les rotations sont définies à l'aide des fonctions trigonométriques sinus et cosinus.
Pour un système de coordonnées à deux dimensions, la matrice de rotation est la suivante :
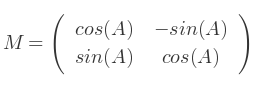
Quand l'angle A est nul, on génère la matrice identité :
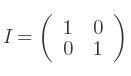
Si A vaut +90 degrés, on a la matrice :
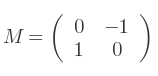
Si l'angle vaut -90 degrés :
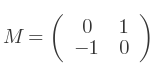
Prendre l'opposé de l'angle revient à transposer la matrice.
Si la matrice de rotation est multipliée par sa transposée, le résultat est la matrice identité.
Utilisez la matrice 4x4 suivante :
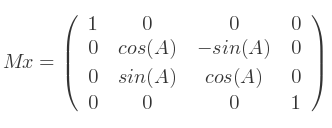
Utilisez la matrice 4x4 suivante :
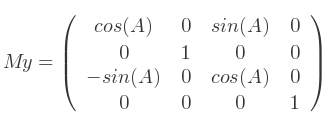
Utilisez la matrice 4x4 suivante :
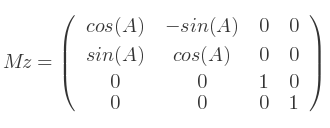
Les angles d'Euler sont le nom donné à un triplet d'angles de rotation (x, y, z) représentant respectivement les rotations autour des axes X, Y et Z.
Exemples :
(0, 0, 0) génèrera la matrice identité (aucune rotation)
(90, 0, 0) est une rotation de 90° autour de X
(30, 0, 55) est une rotation de 30° autour de X, suivie d'une rotation de 55° autour de Z
(0, 80, 90) est une rotation de 80° autour de Y, suivie d'une rotation de 90° autour de ZCes termes sont d'origine aéronautique et correspondent aux rotations à l'aide des angles d'Euler (système de coordonnées euclidien), relativement à la base locale d'un avion.
Imaginez-vous un avion.
L'axe Z passe par la queue et l'avant de l'appareil.
L'axe X part de l'aile gauche à l'aile droite.
L'axe Y pointe vers le haut de l'appareil.
Ainsi le tangage devient la rotation autour de l'axe X, le lacet devient la rotation autour de l'axe Y, et le roulis la rotation autour de l'axe Z.
Les matrices de rotations se combinent en les multipliant entre elles. Attention à l'ordre dans lequel vous les multipliez ! Sinon…
Le problème de la perte d'un degré de liberté, le gmbal lock, arrive quand on utilise les angles d'Euler. Comme la matrice de rotation finale dépend de l'ordre des multiplications, il est possible que parfois, l'une des rotations autour d'un axe soit confondue avec un autre axe de rotation.
Pire encore, il est devient parfois impossible de tourner l'objet suivant un certain axe. C'est le gimbal lock !
Par exemple, supposons qu'un objet est tourné dans l'ordre Z, Y et X et que la rotation autour de Y soit de 90°.
Dans ce cas, la rotation suivant Z se fait correctement, puisque c'est la première. L'axe Y tourne également correctement. Néanmoins, après cette rotation, l'axe X et l'axe Z sont confondus.
Du coup, toute rotation autour de l'axe X tourne l'objet suivant Z ! Pire encore, il est devenu impossible de tourner l'objet autour de l'axe X.
La seule solution à ce problème est de transformer les axes de rotation suivants avec les rotations précédentes. Ces transformations requièrent un outil de combinaison de rotations quelconques, ce qui s'avère plus facile avec des quaternions qu'avec des matrices.
On ne peut pas dire que ce sont les quaternions qui à eux seuls permettent d'éviter le gimbal lock, il est tout à fait possible de reproduire ce problème avec des quaternions.
Autrement dit, si on note R[0x,a](objet) la rotation autour de l'axe 0x et d'angle a de l'objet, R[Oy,b] la rotation autour de l'axe Oy et d'angle b et R[Oz,c] la rotation autour de l'axe Oz d'angle c, pour combiner les trois rotations axiales, on fait :
R(objet)=R[R[R[Ox,a](Oy),b]R[Ox,a](Oz),c](R[R[Ox,a](Oy),b](R[Ox,a](objet)))On conserve ainsi le repère local associé à l'objet qui change après chaque rotation appliqué à celui-ci, on garde ainsi tous les degrés de liberté.
En réalité, il n'y a pas de façon correcte de combiner les matrices de rotation. Néanmoins, afin de prédire les résultats de la combinaison des matrices, un peu d'organisation est nécessaire.
Le moyen le plus simple de tourner un objet est de multiplier les matrices dans cet ordre :
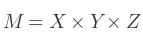
Où M est la matrice de rotation finale, et X, Y, Z les matrices de rotations individuelles.
Néanmoins, quand la vue de la caméra est évaluée, l'ordre et le signe des rotations sont inversés.
Par exemple, si vous êtes debout, et que vous vous tournez vers la droite, tout ce que vous voyez dans votre champ de vision semblera tourner vers la gauche.
Par conséquent, le point de vue de la caméra est modélisé à l'aide de l'ordre suivant :
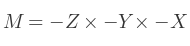
Ceci est l'inverse (ou la transposée) de la matrice de rotation de l'objet.
À première vue, la méthode la plus évidente pour générer une matrice de rotation à partir d'un ensemble d'angles d'Euler est de générer chaque matrice individuellement et de les multiplier ensemble :
m3_rotx(mat_x, vec -> angle_x);
m3_roty(mat_y, vec -> angle_y);
m3_rotz(mat_z, vec -> angle_z);
m3_mult(mat_tmp, mat_z, mat_y);
m3_mult(mat_final, mat_tmp, mat_x);Cet ensemble d'appels peut être placé dans une routine séparée :
m3_fromeuler(MATRIX *mat_final, VECTOR3 *euler)Néanmoins, la réalisation de cette séquence d'appels est vraiment très inefficace en termes de temps de calcul. Étant donné que chaque matrice de rotation 4x4 doit avoir 10 éléments avec la valeur 0, 2 autres avec la valeur 1, et 4 autres avec des valeurs arbitraires, près de 75 % de chaque opération matricielle est fait en pure perte ! Ceci n'inclut pas l'initialisation des matrices…
Un moyen plus efficace doit être trouvé. Heureusement, il existe un autre moyen d'aboutir à la matrice finale.
Si nos trois matrices sont combinées dans un format algébrique, l'expression suivante est définie :
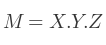
Où :
M est la matrice finale
X est la matrice de rotation autour de l'axe X
Y est la matrice de rotation autour de l'axe Y
Z est la matrice de rotation autour de l'axe Z
Soit les matrices associées :
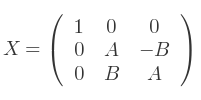
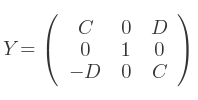
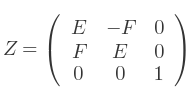
Où A, B sont le cosinus et le sinus de la rotation autour de l'axe X,
C, D sont le cosinus et le sinus de la rotation autour de l'axe Y,
E, F sont le cosinus et le sinus de la rotation autour de l'axe Z.
Alors, l'expression :
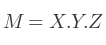
Peut se partager en 2 multiplications de matrices :
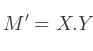
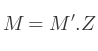
Évaluons M' :
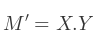
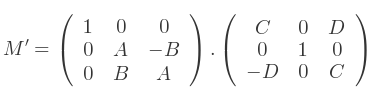
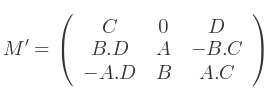
D'où M devient :
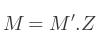
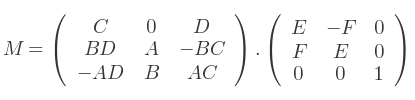
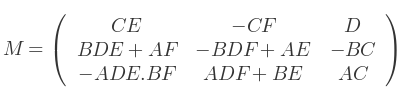
C'est la matrice de rotation finale. En tant que matrice 4x4 :
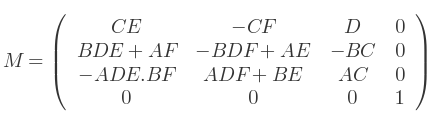
Les valeurs individuelles de A,B,C,D,E et F sont évaluées en premier. Ensuite, on évalue BD et AD puisqu'ils sont fréquents.
Donc, voici l'algorithme final :
A = cos(angle_x);
B = sin(angle_x);
C = cos(angle_y);
D = sin(angle_y);
E = cos(angle_z);
F = sin(angle_z);
AD = A * D;
BD = B * D;
mat[0] = C * E;
mat[1] = -C * F;
mat[2] = D;
mat[4] = BD * E + A * F;
mat[5] = -BD * F + A * E;
mat[6] = -B * C;
mat[8] = -AD * E + B * F;
mat[9] = AD * F + B * E;
mat[10] = A * C;
mat[3] = mat[7] = mat[11] = mat[12] = mat[13] = mat[14] = 0;
mat[15] = 1;À l'aide des multiplications de matrices, on aurait dû faire 128 multiplications, 96 additions et 80 affectations.
Avec cet algorithme, on a fait seulement 12 multiplications, 6 soustractions et 18 affectations !
Donc, par l'utilisation de l'algorithme optimisé, on réalise un gain de 1000 % !
Cette opération est exactement l'opposé de celle vue plus haut. Soit une matrice de rotation :
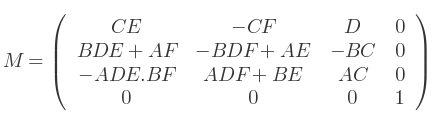
Où A, B sont le cosinus et le sinus de la rotation autour de l'axe X,
C, D sont le cosinus et le sinus de la rotation autour de l'axe Y,
E, F sont le cosinus et le sinus de la rotation autour de l'axe Z.
En utilisant une structure de donnée C pour une matrice 4x4, les valeurs d'index sont les suivants :
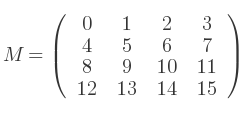
En comparant les deux tables, on constate que l'élément [2] a la valeur de -D, soit -sin(Y). Donc, la rotation autour de l'axe Y peut être calculée à l'aide d'un sinus inverse. Passer le résultat à la fonction cosinus nous donnera la valeur de C.
Si C est non nul, alors la rotation en X et en Z peut être obtenue des termes respectivement sur la troisième et la première colonne :
/* Axe X */
M[6] = -B * C;
M[10] = A * C;
/* Axe Z */
M[0] = C * E;
M[1] = C * -F;Les angles de rotation peuvent être obtenus en prenant chaque paire de valeurs divisées par C et en passant le résultat aux fonctions inverses correspondantes.
Si C est nul, ces calculs sont impossibles. Dans ce cas, l'angle de rotation en Y est de -90 ou de 90°. Donc D vaut 1 ou -1.
Dans ce cas, un gimbal lock s'est produit. Les rotations en X et Z semblent avoir le même axe. Lors du calcul de la matrice, on a :
D'où :
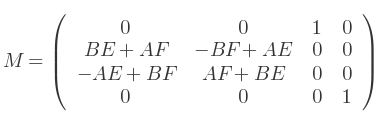
En arrangeant :
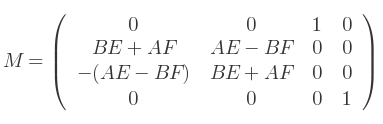
On peut voir la matrice sous cette forme :
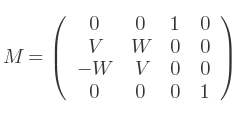
Où :
V vaut BE + AF ;
W vaut AE - BF.
Ces deux valeurs peuvent être vues comme le sinus et le cosinus d'une seule rotation.
L'algorithme final est donc :
angle_y = D = asin(mat[2]); /* Calcul de l'Angle Y */
C = cos(angle_y);
angle_y *= RADIANS;
if (fabs(C) > 0.005) /* Gimbal lock ? */
{
trx = mat[10] / C; /* Non, donc calcul de l'angle X */
try = -mat[6] / C;
angle_x = atan2(try, trx) * RADIANS;
trx = mat[0] / C; /* Calcul de l'angle Z */
try = -mat[1] / C;
angle_z = atan2(try, trx) * RADIANS;
}
else /* Gimbal lock */
{
angle_x = 0; /* Angle X à 0 */
trx = mat[5]; /* Calcul de l'angle Z */
try = mat[4];
angle_z = atan2(try, trx) * RADIANS;
}
angle_x = clamp(angle_x, 0, 360); /* Modulo ;) */
angle_y = clamp(angle_y, 0, 360);
angle_z = clamp(angle_z, 0, 360);La seule façon de générer ce type de matrice de rotation est à l'aide des quaternions.
Voir https://jeux.developpez.com/faq/math/?page=quaternions#Q56 et https://jeux.developpez.com/faq/math/?page=quaternions#Q54.
Quand on développe une application d'animation, une requête commune est de trouver la matrice de rotation qui « mappe » un vecteur direction sur un autre.
Ce problème peut être visualisé en considérant deux vecteurs directions attachés à leur base. Donc, la totalité de l'espace de rotation forme une sphère unité.
En théorie, il existe un nombre infini de rotations possibles pour rendre les deux vecteurs colinéaires. Tous ces axes sont dans le plan pour lequel tous les points appartenant au plan sont à égale distance des deux vecteurs.
Néanmoins, une seule solution est intéressante en pratique. C'est le chemin qui couvre la plus petite distance angulaire entre les deux vecteurs.
L'axe de rotation de ce chemin se calcule à l'aide du produit vectoriel entre les deux vecteurs :
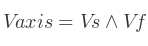
L'angle de rotation est calculé à l'aide du produit scalaire entre les deux vecteurs :

Attention, si ceux-ci ne sont pas normalisés il faudra tenir compte de leur norme dans le calcul :
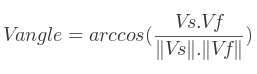
Cependant, l'angle obtenu n'est pas forcément correct : en effet un cosinus peut être obtenu avec deux angles différents (cos(x) = cos(-x)). Il faudra donc trouver un moyen de déterminer s'il s'agit de x ou -x.
De façon similaire au problème précédent, nous avons besoin de « confondre » deux systèmes de coordonnées. Néanmoins, il s'agit de faire correspondre trois axes au lieu d'un seul. Les deux systèmes sont représentés par des matrices 3x3 ou 4x4.
Le problème est donc de trouver la matrice de rotation qui va réaliser cette tâche. On peut l'exprimer mathématiquement comme :
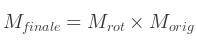
Où :
Mfinale est la matrice du système de coordonnées final,
Morig est le système de coordonnées original et
Mrot est la matrice de rotation voulue.
L'objectif est de trouver Mrot. Ceci peut être fait en réécrivant l'équation comme suit :

Ainsi, la matrice de rotation peut être calculée via la multiplication de la matrice finale avec l'inverse de la matrice de départ.
Une fois calculée, cette matrice de rotation peut être conservée dans un quaternion.
Une matrice de translation sert à positionner un objet dans l'espace sans le tourner. Les translations en 3D sous forme matricielle ne peuvent être réalisées qu'avec des matrices 4x4 (voir https://jeux.developpez.com/faq/math/?page=bases#Q1).
Si la translation se définit par un vecteur (X, Y, Z), alors on a la matrice 4x4 suivante :
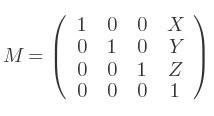
Si le vecteur est (0, 0, 0) alors la matrice correspondante est l'identité, et l'objet n'est pas modifié.
C'est une matrice qui permet de grossir ou de rapetisser un modèle 3D.
Si le vecteur de mise à l'échelle est (X, Y, Z) alors la matrice qui correspond est la suivante :
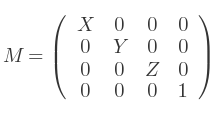
Si le vecteur de mise à l'échelle est (1, 1, 1), alors on obtient la matrice identité et l'objet ne change pas.
C'est une matrice qui permet de faire en sorte qu'un modèle 3D apparaisse « penché », comme les caractères italiques par exemple.
En 3 dimensions, 6 directions de déformation existent :
- Étirer X selon Y ;
- Étirer X selon Z ;
- Étirer Y selon X ;
- Étirer Y selon Z ;
- Étirer Z selon X ;
- Étirer Z selon Y.
Ces 6 transformations peuvent se combiner dans une seule matrice :
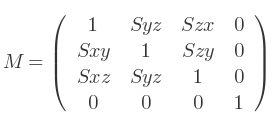
Où Sij représente une déformation de l'axe I selon l'axe J.
Étant donné deux matrices de transformation, le problème est de trouver le moyen de déterminer les positions intermédiaires par une variable paramétrique t, avec t variant de 0.0 à 1.0.
Ceci peut se faire en convertissant les deux matrices en angles d'Euler ou sphériques (quaternions) et un vecteur translation.
Dans les deux cas, chaque matrice est convertie en une paire de vecteurs 3D.
L'interpolation entre chacun de ces deux vecteurs peut être réalisée via l'équation d'interpolation linéaire classique :
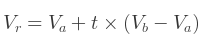
Où :![]() est le vecteur résultant
est le vecteur résultant![]() est le vecteur position de départ
est le vecteur position de départ![]() est le vecteur position finale
est le vecteur position finale
Cette équation s'applique aussi bien aux vecteurs de la translation qu'à celui de la rotation.
Une fois déterminées, la translation et la rotation résultantes sont converties dans la matrice intermédiaire voulue.
Étant donné quatre matrices, le problème consiste à trouver un moyen pour déterminer les positions intermédiaires spécifiées par la variable paramétrique t.
Ceci peut être réalisé en faisant usage de l'interpolation cubique. Comme pour l'interpolation linéaire, les quatre matrices sont converties dans leurs vecteurs rotations et translations correspondants (Euler ou sphérique).
Chaque ensemble de 4 vecteurs est alors converti en un unique vecteur géométrique G. À l'aide des mathématiques des splines, ce vecteur est converti en une matrice d'interpolation M.
Si G est défini comme tel :
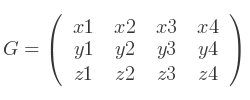
Alors, la multiplication par la matrice de base :
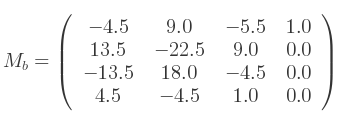
Va générer une matrice d'interpolation 3x4 Mi :
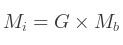
Ceci peut être implémenté à l'aide d'une multiplication standard matrice-vecteur.
L'interpolation peut être faite par l'usage de la variable paramétrique t :
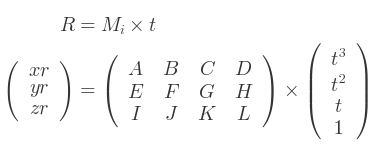
Le vecteur résultant peut être converti en une matrice de rotation ou de translation.
Il doit être noté que les chemins de rotation générés peuvent sembler quelque peu acrobatiques. C'est normal dans le sens que l'algorithme essaye de trouver le chemin avec le minimum de rotations entre les 4 vecteurs.
Des angles d'Euler ou sphériques, ces derniers semblent en général être plus « propres » pour cette interpolation.