Une matrice est un outil mathématique utilisé dans beaucoup de domaines, dont la 3D. On peut les représenter comme un tableau à deux dimensions contenant des valeurs scalaires (entières, réelles ou complexes).

On peut réaliser sur les matrices des opérations proches de celles que l'on applique sur les nombres réels comme l'addition, la soustraction, la multiplication ou l'inversion. Cependant à cause de leur nature plus complexe certaines de ces opérations peuvent être définies de plusieurs façons différentes. Par exemple la multiplication peut être membre à membre ou utiliser une formule qui multiplie les lignes de l'une contre les colonnes de l'autre.

Une matrice avec M lignes et N colonnes est appelée une matrice MxN.

Les éléments d'une matrice peuvent être référencés à l'aide de deux valeurs d'index. La notation mathématique « classique » les assigne aux variables 'i' (lignes) et 'j' (colonnes).

Par exemple, si l'on considère une matrice de taille 4x4, alors les éléments de la matrice sont indéxés par les couples lignes|colonnes :

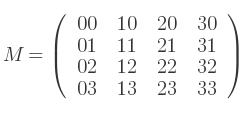
L'élément en haut à droite de la matrice, à i = 0 et j = 3, est identifié comme suit :

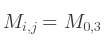
Une matrice n'est pas seulement un tableau de valeurs, mais elle représente une transformation d'un espace de départ vers un espace d'arrivée. Si par exemple, on a un vecteur colonne à deux dimensions, alors on peut définir le vecteur colonne transformé dans un espace à trois dimensions comme la multiplication d'une matrice 2x3 par ce vecteur colonne (pour la multiplication on peut considérer le vecteur colonne comme une matrice 1x2). Une telle transformation est appelée linéaire parce qu'elle respecte certaines propriétés comme la conservation des facteurs d'échelle (et a un point fixe qui est l'origine).

Les matrices les plus utilisées en informatique graphique sont donc celles qui transforment les vecteurs à deux dimensions ou à trois dimensions. Cela inclut notamment les matrices 2x2 qui représentent les transformations linéaires du plan 2D (rotation, mise à l'échelle autour de l'origine, miroir), et les matrices 3x3 qui représentent les transformations linéaires de l'espace en 3D (rotation, mise à l'échelle autour de l'origine, miroir).

Les matrices que traitent les cartes graphiques dans la partie « transformation et éclairage » sont des matrices 4x4. La raison d'être de ces matrices, c'est qu'elles représentent de manière très pratique certaines opérations non linéaires dans l'espace en 3D (translation, projection conique sur un plan), en ajoutant une quatrième coordonnée (la coordonnée homogène).

Nous n'allons pas détailler ce que sont les coordonnées homogènes et les espaces projectifs qui y sont associés, mais pour faire simple, il y a une loi qui permet de passer de l'espace 3D à l'espace homogène et vice versa :

coordonnées 3D -> coordonnées homogènes :
(x, y, z) -> (x, y, z, 1)

coordonnées homogènes -> coordonnées 3D :
(x, y, z, w) -> (x/w, y/w, z/w).

Comme dit précédemment, c'est une transformation non linéaire, mais qui permet en contrepartie d'extraire la partie « linéaire » d'opérations comme la translation et la projection conique. Ces deux opérations étant parmi les plus courantes en 3D par ordinateur, il est donc logique que les cartes graphiques les accélèrent.

On peut également rajouter une troisième coordonnée « homogène » à des coordonnées 2D pour les mêmes raisons.

On peut également utiliser des matrices beaucoup plus larges pour des applications comme le traitement d'images (convolutions), le calcul de probabilités (chaines de Markhov), l'intelligence artificielle (les réseaux de neurones), l'algorithmique de base (recherche sur les graphes), etc. C'est l'outil de base du scientifique.

L'ordre d'une matrice est l'autre dénomination de la taille d'une matrice. Une matrice à M lignes et N colonnes est dites d'ordre MxN.

Les représentations des matrices peuvent être différentes d'un programme à un autre. Il faut notamment faire attention aux conventions sur les notations qui, si elles sont mélangées, apporteront leur lot de bogues dans vos programmes.

En C et en C++, il y a une manière naturelle de représenter un tableau, via un tableau de flottants à deux dimensions :

float matrice[10][10];

Ce qui permet de se référer à l'élément m(i,j) par un simple

m_ij = matrice[i][j];

Ce n'est évidemment pas la seule manière possible, on peut se référer aux éléments d'une matrice dans un tableau à une seule dimension :

float matrice[100];

Et accéder aux éléments avec un calcul un peu plus complexe :

m_ij = matrice[i + j * 10];

C'est là que la convention est importante, parce que l'on aurait tout aussi bien pu y accéder par :

m_ij = matrice[i * 10 + j];

Il est également possible de nommer chaque élément séparément et les réunir dans une structure ou une classe. Ou encore, les nommer par colonnes ou par lignes en conservant la notation tableau.

struct Matrice1
{
  float _11, _12, _13;
  float _21, _22, _23;
  float _31, _32, _33;
};

struct Matrice2
{
  float ligne1[3];
  float ligne2[3];
  float ligne3[3];
};

Vous rencontrerez probablement toutes ces notations suivant les programmes et parfois mélangées pour tirer parti de la meilleure performance de l'un (passer les vecteurs colonnes/lignes directement), ou la plus grande facilité à déboguer de l'autre.

Enfin, en C++, on essaye généralement d'encapsuler toutes ces considérations dans des classes qui implémentent des méthodes permettant de réaliser les opérations usuelles sans se soucier de la représentation interne (la meilleure solution de toute évidence).

Attention aux conventions, si l'API prévoit que les éléments d'un vecteur colonne sont adjacents en mémoire on essaye en général de choisir la même convention que celle de l'API que l'on utilise, pour des raisons pratiques et pour éviter des bogues de conversions. Mieux : certaines API par exemple Direct3D proposent en standard une classe MATRIX qu'il est sans doute intéressant de réutiliser lorsque l'on démarre un programme à partir de zéro.

Pour les autres, il existe également de nombreuses bibliothèques indépendantes permettant de manipuler les matrices :

• boost::uBLAS (C++)
• MTL (C++)

L'une des premières questions sur les matrices est : « pourquoi sont-elles tellement utilisées en informatique ? » Intuitivement, il semble que la surcharge due aux boucles for et aux multiplications de matrices devrait plus ralentir l'application qu'autre chose.

Cette objection ne tient pas compte de l'utilisation des registres CPU pour gérer les compteurs et des caches de données qui optimisent l'accès mémoire.

De plus, en suivant une approche mathématique pour définir les algorithmes 3D, il est possible de prévoir et de planifier le design d'un système d'animation 3D. Une telle approche permet très simplement d'envisager l'implémentation de l'animation des personnages, des courbes splines, de la cinématique inverse…

Néanmoins, une des objections qui revient fréquemment est qu'il serait plus rapide de juste multiplier chaque paire de coordonnées par les coefficients de rotation pour cet axe, au lieu de réaliser une multiplication vecteur/matrice.

C'est-à-dire :

rotation en X transforme Y et Z ;
rotation en Y transforme X et Z ;
rotation en Z transforme X et Y.

Ce qui revient à ceci :

Soient un vertex V = (x, y, z), les angles de rotation (A, B et C) et les translations (D, E, F). L'algorithme est défini comme suit :

sx = sin(A)             // Setup - une seule fois
cx = cos(A)
sy = sin(B)
cy = cos(B)
sz = sin(C)
cz = cos(C)

x1 = x                  // Rotation de chaque vertex
y1 = y * cx - z * sx
z1 = y * sx + z * cx

x2 = x1 * cy + z1 * sy
y2 = y1
z2 = z1 * cy - x1 * sy

x3 = x2 * cz - y2 * sz
y3 = x2 * sz + y2 * cz
z3 = z2

xr = x3 + D             // Translation de chaque vertex
yr = y3 + E
zr = z3 + F

Voici le taux de calcul pris par cet algorithme :

Admettons qu'il est possible de réaliser la même chose par des multiplications de matrices…

Pour une matrice 4x4, on a :

En comparant les deux tables, on peut constater que la préparation d'une matrice de rotation coûte au moins 12 multiplications et 12 affectations en plus.

Néanmoins, alors que cela peut sembler étrange, l'économie vient du calcul de chaque vertex. En utilisant la multiplication de matrice, l'économie faite en calculant juste 4 vertex rattrape la dépense faite plus haut !

La relation entre les matrices 3x3 ou 4x4 et le système de coordonnées est simple.

Les 3 premières colonnes de la matrice définissent les vecteurs direction respectivement des axes X, Y et Z.

Si une matrice 4x4 est définie en tant que :

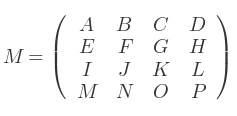
Alors, le vecteur direction pour chaque axe est le suivant :

• Axe X = [A E I]
• Axe Y = [B F J]
• Axe Z = [C G K]