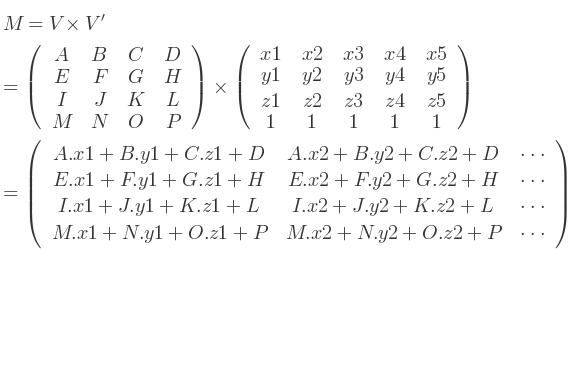FAQ mathématiques pour les jeux

FAQ mathématiques pour les jeuxConsultez toutes les FAQ
Nombre d'auteurs : 7, nombre de questions : 82, dernière mise à jour : 15 juin 2021
 Sommaire→Matrices→Arithmétique
Sommaire→Matrices→Arithmétique- Qu'est-ce que la matrice identité ?
- Qu'est-ce que la diagonale d'une matrice ?
- Qu'est-ce que la transposée d'une matrice ?
- Comment ajouter deux matrices ?
- Comment soustraire deux matrices ?
- Comment multiplier deux matrices ?
- Comment élever une matrice à une puissance quelconque ?
- Comment multiplier un ou plusieurs vecteurs par une matrice ?
La matrice identité est une matrice qui a autant de colonnes que de lignes, et pour laquelle tous les éléments tels que i = j valent 1 et les autres 0. Par exemple :

La diagonale principale d'une matrice est l'ensemble des éléments pour lesquels le numéro de la ligne est égal à celui de la colonne (Mij où i = j).
Dans le cas de la matrice identité, seuls les éléments sur la diagonale sont mis à la valeur 1, tandis que les autres sont à 0.
La transposée d'une matrice M, notée MT, est la matrice générée par l'inversion des éléments de la matrice d'origine par rapport à la diagonale :
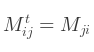
Cette opération est valable sur toutes les matrices, carrées ou non.
Soit M :
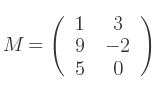
La transposée de M est :
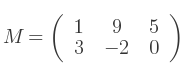
Si la matrice est une matrice de rotation, la transposée est la rotation inverse.
L'addition peut s'exprimer comme suit :
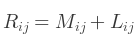
Néanmoins, les deux matrices doivent être de taille identique.
Par exemple :
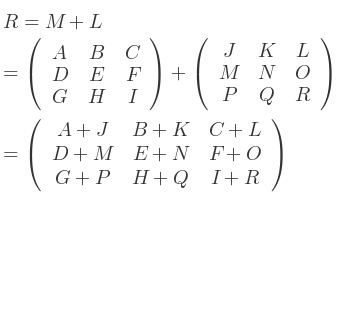
Cette opération est aussi simple que l'addition :
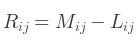
Néanmoins, les deux matrices doivent être de tailles identiques.
Par exemple :
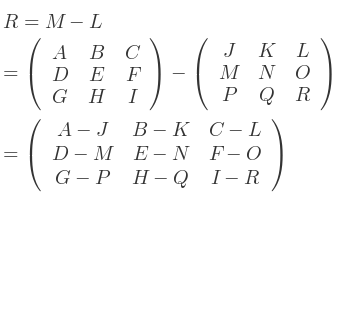
Il faut multiplier chaque élément d'une ligne de la première matrice avec chaque élément d'une colonne de la seconde et faire la somme.
On peut l'exprimer comme suit :
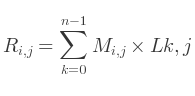
Si les deux matrices sont d'ordres :
M = AxB et L = CxD
Alors les deux valeurs B et C doivent être identiques.
Dans ce cas, la matrice résultante est d'ordre AxD.
De plus, il est possible de multiplier une matrice 4x4 par une matrice 4xN, mais pas l'inverse.
Par exemple, si M est définie par :
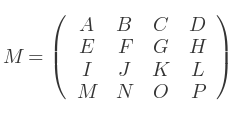
et L par :
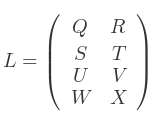
Alors, la taille de la matrice résultante est 2x4 :
Une matrice peut être élevée à n'importe quelle puissance entière. Néanmoins, il y a plusieurs restrictions. Pour chaque puissance, la matrice doit rester carrée, i.e. avoir le même nombre de lignes et de colonnes.
Par exemple,
- M-1 est l'inverse de la matrice.
- M0 génère la matrice identité
- M1 ne modifie pas la matrice
- M2 élève la matrice au carré
- M3 élève la matrice au cube
Élever une matrice à une puissance supérieure à 1 revient à la multiplier par elle-même un nombre spécifique de fois.
Par exemple,
- M2 = M x M
- M3 = M x M x M
Élever la matrice identité à n'importe quelle puissance conserve la matrice identité : In = I.
Le meilleur moyen de réaliser cette tâche est de traiter la liste de vecteurs comme une simple matrice, dont chaque vecteur représente un vecteur colonne.
Si N vecteurs doivent être multipliés par une matrice 4x4, ils peuvent être traités comme une unique matrice 4xN :
Soit la matrice :
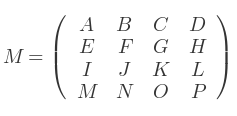
Et la liste de vecteurs suivante :
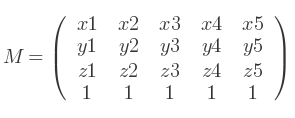
Remarquez qu'une ligne de termes constants est ajoutée à la liste de vecteurs, tous à 1. Cette ligne ne devrait pas exister. C'est simplement pour permettre la correspondance entre les ordres de M et de V.
Exemple de multiplication :
Pour chaque vecteur de la liste, il y aura un total de 12 multiplications, 16 additions et 1 division (pour la perspective).
Si la matrice est une matrice de rotation ou de translation, la division peut être annulée.