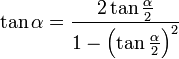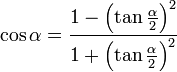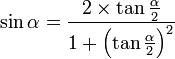IdentifiantMot de passe
Mot de passe oublié ?Je m'inscris ! (gratuit)

FAQ mathématiques pour les jeux

FAQ mathématiques pour les jeuxConsultez toutes les FAQ

Nombre d'auteurs : 7, nombre de questions : 82, dernière mise à jour : 15 juin 2021 

 
OuvrirSommaire→Trigonométrie→Relations trigonométriques
précédentsommairesuivant
 Version PDF Version hors-ligne 
 
 
HautPage
Comment calculer le sinus ou le cosinus d'une somme ou d'une différence ?

Il existe six formules d'addition et de soustraction de base en trigonométrie ; les voici dans une version condensée.

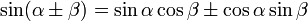
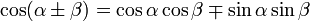
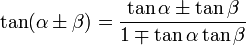
Image non disponible
Image non disponible
Image non disponible
Créé le 16 septembre 2010  par Thibaut Cuvelier
 
HautPage
Comment factoriser ou distribuer une expression trigonométrique ?

On utilise généralement en ce but les formules de Simpson, qui peuvent être lues dans un sens ou dans l'autre afin d'obtenir les deux sens : distribution ou factorisation.

Au contraire des autres identités trigonométriques, les variables utilisées sont p et q.

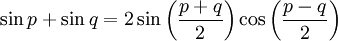
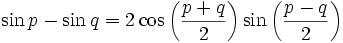
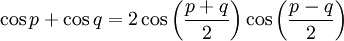
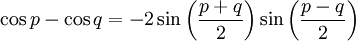
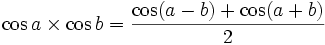
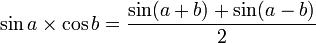
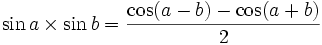
Image non disponible
Image non disponible
Image non disponible
Image non disponible
Image non disponible
Image non disponible
Image non disponible
Créé le 16 septembre 2010  par Thibaut Cuvelier
 
HautPage
Comment calculer les nombres trigonométriques d'un double d'angle ?

Ces formules sont des cas particuliers des formules d'addition et de soustraction d'angles. En effet : x + x = 2x.

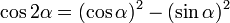
\cos{2\alpha} = (\cos{\alpha})^2 - (\sin{\alpha})^2
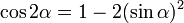
\cos{2\alpha} = 1 - 2(\sin{\alpha})^2
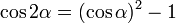
\cos{2\alpha} = (\cos{\alpha})^2 - 1
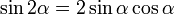
\sin{2\alpha} = 2\sin{\alpha} \cos{\alpha}
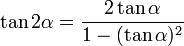
\tan{2\alpha} = \frac{2\tan{\alpha}}{1-(\tan{\alpha})^2}
Créé le 16 septembre 2010  par Thibaut Cuvelier
 
HautPage
Comment exprimer les nombres trigonométriques en fonction de la tangente de la moitié d'un angle ?

Il suffit de transformer les identités précédentes afin de faire ressortir des tangentes.

\tan\alpha=\frac{2\tan{\frac{\alpha}{2}}}{1-\left(\tan\frac{\alpha}{2}\right)^{2}}
\cos{\alpha}=\frac{1-\left(\tan\frac{\alpha}{2}\right)^{2}}{1+\left(\tan\frac{\alpha}{2}\right)^{2}}
\sin{\alpha}=\frac{2\times\tan\frac{\alpha}{2}}{1+\left(\tan\frac{\alpha}{2}\right)^{2}}
Créé le 16 septembre 2010  par Thibaut Cuvelier
précédentsommairesuivant
 Version PDF Version hors-ligne 
 

Les sources présentées sur cette page sont libres de droits et vous pouvez les utiliser à votre convenance. Par contre, la page de présentation constitue une œuvre intellectuelle protégée par les droits d'auteur. Copyright © 2005-2014 Developpez LLC et al. Aucune reproduction, même partielle, ne peut être faite de ce site ni de l'ensemble de son contenu : textes, documents, images, etc. sans l'autorisation expresse de l'auteur. Sinon vous encourez selon la loi jusqu'à trois ans de prison et jusqu'à 300 000 € de dommages et intérêts.