Navigation▲
| Tutoriel précédent : gestion des décors | Sommaire | Tutoriel suivant : sprites enrichis |
II. Introduction▲
Nous allons voir ici quelques algorithmes qui permettent, non pas de tester directement des collisions, mais d'optimiser les calculs de façon à faire beaucoup moins de tests, et donc aller beaucoup plus vite.
III. Problématique▲
Avant de poursuivre, je vous laisse lire le chapitre précédent sur la collision Segment-Segment, et l'exemple de Doom que j'ai pris.
La carte d'un petit niveau de Doom donne ceci :
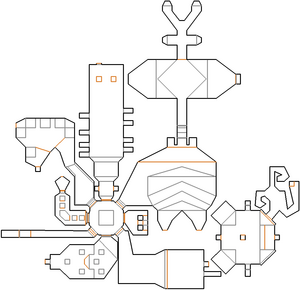
Les murs sont des segments en noir, les « marches » sont en gris ou en orange.
Quand nous nous déplaçons dans cette carte, nous testons des collisions Segment-Segment, comme nous avons vu dans le chapitre du même nom.
Mais si on veut être sûr de ne pas passer à travers un mur, il faut tous les tester ! Et à chaque mouvement !
Même si le test est rapide, tester 100, 1000, 10 000 ou même 100 000 murs, car un niveau peut être grand, ce sera beaucoup trop violent.
Il va donc falloir tester les murs « autour » du joueur, et pas les autres. En effet, si je suis complètement à droite du niveau, tester tous les murs à gauche est stupide.
Mais comment va-t-on faire pour cela ? Nous allons voir plusieurs méthodes.
IV. La grille▲
L'idée la plus simple est de définir une grille.
IV-A. Boîte englobante▲
Tout d'abord, un niveau, aussi grand soit-il, est inscrit dans une boîte englobante, une AABB.
Pour la calculer, c'est simple, il suffit de parcourir tous les segments, et de relever les x et y, et de garder le minimum et le maximum.
Ceci est calculatoire, mais ne sera fait qu'une seule fois (au chargement de la carte) voire, encore mieux, sera carrément fourni avec la carte si on a calculé cela au moment où on l'a créée, et qu'on a enregistré le résultat avec elle.
Voici donc la carte avec sa boîte englobante :

IV-B. Découpage▲
L'idée de la grille va être très simple : nous découpons la boîte englobante en petits carrés égaux en taille. Cela nous donne ceci :
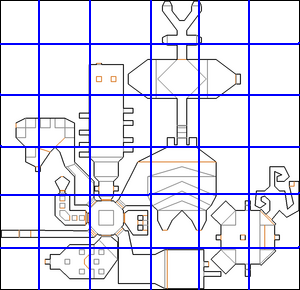
Dans cet exemple, j'ai découpé en 36 morceaux (6 * 6).
Et dans chaque morceau, je vais stocker la liste de mes segments.
Il y aura donc 36 listes (ou tableaux) de segments, répartis dans un tableau 2D de « petits carrés ».
En mémoire, on pourra avoir ceci :
struct Segment // un segment, c'est 2 points
{
Point A,B;
};
struct Carre // un carré contient une liste (ou tableau) de segments
{
Segment* tableau;
int nbsegs;
};
struct Grille // tableau à deux dimensions
{
Carre** c; // en autre langage que le C, on pourra écrire Carre[nbx][nby] c;
int nbx,nby;
float largeurcarre,hauteurcarre;
AABB bbox; // boîte englobante globale, de tout le niveau
};Pour créer la grille, le concept est le suivant : nous avons notre niveau au départ avec un grand tableau de segments (tous les segments du niveau).
On les prend un par un, et on les range dans le bon carré, en fonction de leur position.
Notez que tout ceci se fait également une fois pour toutes
- soit pendant le chargement de la carte ;
- soit ces données sont enregistrées avec la carte, et ont été calculées lors de la création de la carte.
Dans les deux cas, une fois dans la boucle du jeu, nous n'aurons plus à faire ces calculs, donc le jeu sera rapide.
IV-B-1. Calcul de la largeur et hauteur d'un carré▲
Étant donné la boîte englobante AABB du niveau, et le nombre de carrés en x et en y que l'on souhaite, une simple division permet de calculer la largeur et la hauteur d'un carré :
Grille.largeurcarre = bbox.w/nbx;
Grille.hauteurcarre= bbox.h/nby;
IV-B-2. Dans quel carré est mon point P▲
Vous avez un point P, vous voulez savoir dans quel carré il est. Un peu comme le tilemapping, c'est une histoire de mise à l'échelle. Notez que, contrairement à un tilemapping bien fait, l'origine de la grille n'est pas (0,0) mais bien le point min de la boîte englobante (bbox.x;bbox.y).
Donc pour un point P (Px,Py) donné, nous avons :
i = (Px-bbox.x)/largeurcarre;
j = (Py-bbox.y)/hauteurcarre;
Il faut prendre la partie entière de i et j pour savoir dans quel carré est le point P.
IV-B-3. Segment inscrit▲
Nous disions donc, pour préparer nos 36 listes, que nous prenons les segments un par un. Un segment, c'est deux points A et B.
Nous calculons rapidement dans quel carré sont A et B grâce au calcul ci-dessus.
Si les deux points sont dans le même carré, c'est formidable, le segment est inscrit dans le carré, nous l'ajoutons à la liste du carré correspondant.
Dans le cas contraire, il y a chevauchement du segment au-dessus de plusieurs carrés.
IV-B-4. Chevauchement▲
En effet, si les deux points du segment ne sont pas dans le même carré, cela pose problème.
Pour éviter ce problème, nous allons découper le segment en plusieurs segments.
Pour cela, nous calculons l'intersection entre le segment et les bords des carrés concernés, et nous mettons deux ou plusieurs petits segments ainsi formés dans chacun des carrés correspondants.
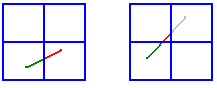
Sur ce dessin, à gauche j'ai un segment coupé une fois : je coupe et je mets donc le segment vert dans la liste du carré de gauche, et le segment rouge dans la liste du carré de droite.
À droite, le segment coupe trois carrés. Je coupe et je mets donc les segments vert, rouge et gris dans les listes des carrés correspondants.
À la fin de cette étape-là, chaque carré contient sa propre liste de murs. La construction de la grille est terminée.
IV-C. Calcul de collision▲
Maintenant que notre grille est prête, comment tester si notre personnage de Doom touche un mur ?
Eh bien l'idée est la suivante :
nous avons vu que le déplacement d'un personnage de doom est un segment. Il va falloir déterminer dans combien de carrés ce segment va passer.
Et pour chacun de ces carrés de passage, on va tester la collision avec la liste de ses murs ;
il sera ainsi inutile de tester la collision avec les carrés où on ne passe pas : ils sont suffisamment loin pour qu'on ne les touche pas.
C'est ainsi qu'on restreint très fortement le nombre de tests, en ne testant que les murs autour de notre trajectoire.
IV-D. Inconvénients▲
Cette méthode présente quelques inconvénients.
Il faut déterminer le nombre de carrés que l'on veut, donc fixer nbx et nby au départ.
Si on fixe des valeurs petites, alors les carrés seront grands, et pourront donc contenir des listes de segments à tester assez grandes. Si par exemple, dans un carré, on a 1000 murs à tester, parce qu'on a une pièce petite avec beaucoup d'obstacles, ça fait beaucoup de tests.
Si on fixe des valeurs grandes, et qu'ainsi on se retrouve avec une grille assez fine, alors on fait exploser le nombre de carrés à stocker… avec leurs listes ! Ça consommera donc énormément de mémoire.
Si la carte se compose d'une petite maison avec beaucoup de murs, et à côté d'un très grand terrain : on aura plein de carrés avec une liste vide pour le terrain, mais qui couteront quand même de la mémoire.
V. Le quadtree▲
Le quatree est un autre système de partitionnement qui présente des avantages par rapport à la grille.
V-A. Présentation▲
Avant tout, le terme Quadtree veut dire « Arbre à quatre fils ». Cette partie nécessite de connaître la notion d'arbre en informatique.
Reprenons notre terrain, avec sa boîte englobante AABB, comme vu dans le chapitre au-dessus.
Maintenant, observons le dessin ci-dessous :
Il est composé de trois cartes. Regardons à gauche.
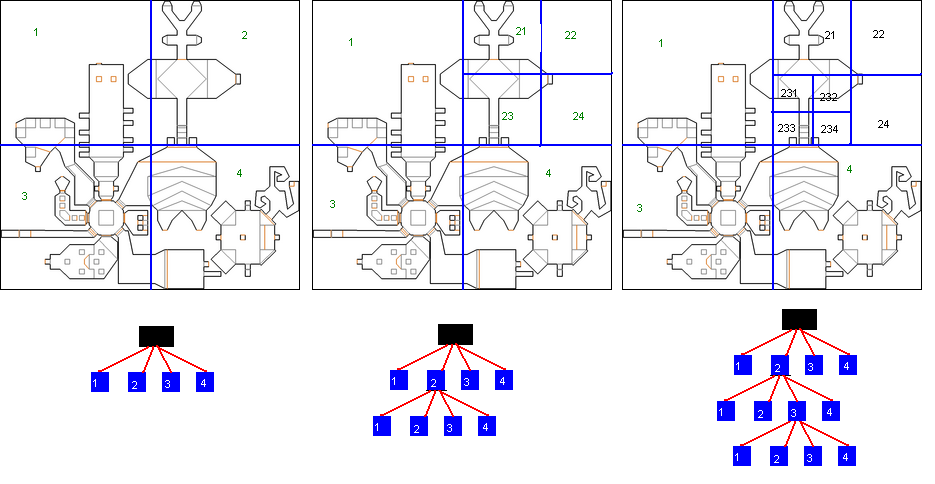
J'ai coupé en quatre parts égales la carte (les traits bleus), en coupant au milieu de la boîte englobante globale. J'appelle les nouvelles zones ainsi créées 1,2,3,4.
En mémoire (si on regarde en dessous), j'ai un arbre, à quatre fils. La racine, c'est « le monde entier », chacun des fils est une des quatre zones ainsi créées.
Pour le moment, c'est exactement comme si j'avais fait une grille avec nbx = 2 et nby = 2, sauf que je range ça dans un arbre.
Je dis, arbitrairement, que le 1er fils est le carré en haut à gauche, le 2e celui en haut à droite, le 3e celui en bas à gauche, le 4e celui en bas à droite. Je mets l'ordre que je veux, mais il faudra s'y tenir.
Maintenant, regardons le dessin du milieu. Je n'ai pas touché à mes zones 1,3,4, mais pour la zone 2, je l'ai encore découpée en 4, en coupant de nouveau la zone au milieu. Me voilà avec 4 nouvelles zones que j'ai appelées 21,22,23,24. Ces zones sont des filles de la zone 2 (puisque c'est la zone 2 que j'ai découpée).
Je suppose que vous commencez à comprendre le concept. Le 3e dessin redivise à nouveau la zone 23 en 4 nouvelles zones, en coupant la zone mère en son milieu.
Et je peux continuer comme cela autant que je veux…
Et à la fin, comme dans l'algorithme de la grille, je vais ranger un tableau de murs dans chaque feuille de mon arbre, donc dans les zones terminales.
En mémoire, cela se présente ainsi :
struct QuadTree
{
AABB bbox; // bounding box du noeud
QuadTree* fils[4]; // 4 fils.
Segment* tableau;
int nbsegs;
};L'arbre est un nœud, la racine contient la boîte englobante du monde, chaque fils contient une boîte englobante quatre fois plus petite (deux fois en x, deux fois en y) que son père.
Quand on arrive sur une feuille, les quatre pointeurs vers les Quadtree fils seront à NULL.
Ces pointeurs seront soit tous nuls, soit tous non nuls.
Du coup, pour vérifier qu'un nœud est une feuille, il suffira de regarder le premier fils, et voir s'il est nul ou non.
Mais uniquement les feuilles du quadtree pourront contenir des segments, pas les nœuds intermédiaires. (Il existe des variantes de quadtrees qui pourraient permettre ça, mais on n'en parlera pas ici.)
V-B. Découpage▲
Comment découper un Quadtree ? Jusqu'où continuer à découper, à l'infini ?
L'idée est de définir une variable NBMAX qui sera le nombre maximal de segments qu'on veut dans une liste. Par exemple, je dis que chaque zone ne contiendra pas plus de 10 segments à tester.
Donc au début, je construis la racine du quadree. Je mets tous mes segments dedans (dans la liste du nœud). Disons 1000 segments.
Est-ce qu'il y a plus de segments que NBMAX ? Oui, évidemment. Alors je découpe : je crée quatre fils, et je vais distribuer les segments dans chacune des quatre listes des quatre fils.
Je considère une extrémité de segment, disons un point P. Comment savoir dans quelle zone il devra aller ?
Il suffit de prendre la boîte englobante du père, et de prendre son point milieu I.
- Si Px < Ix et Py < Iy alors on ira dans le fils 1.
- Si Px > Ix et Py < Iy alors on ira dans le fils 2.
- Si Px < Ix et Py > Iy alors on ira dans le fils 3.
- Si Px > Ix et Py > Iy alors on ira dans le fils 4.
Je vide ainsi la liste du père, pour répartir tous les segments dans les 4 fils.
Si mon découpage coupe en deux quelques segments, je crée des segments plus petits, comme pour la grille.
J'aurais donc potentiellement plus de 1000 segments à distribuer.
Au vu de la carte, disons que j'en distribue 150 au fils 1, 200 au fils 300 au fils 3 et 400 au fils 4.
(j'en ai injecté 1050 à cause des chevauchements).
Je continue récursivement sur chaque zone. Chaque zone a plus de NBMAX éléments dans sa liste, donc je les découpe toutes à nouveau…
Arrivé au 3e niveau, je constate que la zone 1_1 n'a pas de segments, et que la zone 1_2 en a cinq : j'arrête donc de subdiviser ces zones. Mais pour le reste je continue…
Je me retrouve donc avec un bel arbre, qui, pour chaque nœud, a quatre fils, et au bout, ses feuilles n'ont pas plus de NBMAX éléments.
Note : dans certains cas extrêmes, on pourra arrêter les découpages quoi qu'il arrive, même s'il y a trop de segments dans la liste, si on arrive au-delà d'une profondeur maximale fixée…
La construction d'un Quadtree se fait au chargement d'une carte, ou bien est enregistrée avec la carte directement. Tous ces calculs sont déjà faits et ne sont plus à refaire quand le jeu tourne.
V-C. Calcul de collision▲
Le calcul de collision depuis un quadtree revient uniquement à déterminer les feuilles où passe notre trajectoire. On a un segment qui représente notre trajectoire, on le fait descendre dans le quadtree comme on faisait descendre les murs, on se retrouve avec le segment dans une feuille (ou plusieurs s'il a été découpé).
Il suffira de tester les collisions avec les listes de segments murs des feuilles considérées…
V-D. Inconvénients▲
L'inconvénient du quadtree est son potentiel déséquilibre. En effet, si notre carte contient des zones denses, et d'autres vides, l'arbre va être déséquilibré.
Prenons un cas extrême : une carte est un grand terrain avec une petite cabane dans un coin, mais une cabane avec beaucoup de murs.
Le quadtree associé aura quatre fils, trois avec quasiment aucun mur, et il faudra descendre fort profond pour trouver la cabane, qui, étant petite, sera dans une zone petite, donc profonde dans l'arbre. Le reste de l'arbre sera presque vide.
VI. Le BSP 2D▲
Le BSP 2D est une très bonne réponse à ces inconvénients.
VI-A. Présentation▲
BSP signifie « Binary Space Partitionning », autrement dit : « on coupe l'espace en deux ».
Le BSP se base sur des arbres binaires : donc des arbres à deux fils.
Regardons le schéma ci-dessous :
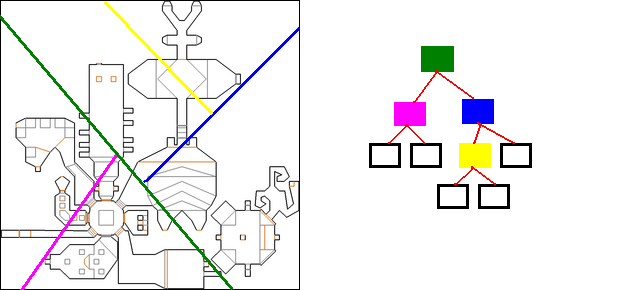
Nous retrouvons, à gauche, notre carte. Je l'ai d'abord coupée en deux par un grand trait vert. D'un côté du trait vert, j'obtiens donc une zone, que je coupe à nouveau avec un trait violet, et j'arrête le découpage de ce côté-là.
Regardez à droite l'arbre : la racine est verte, comme le premier trait vert que j'ai tracé, puis, d'un côté de l'arbre, j'ai mis un nœud violet pour symboliser le découpage de cette moitié en deux. Puis j'ai mis les feuilles en dessous de la zone violette.
Si on regarde l'autre côté du trait vert, là où il y a le trait bleu, on voit que je coupe la zone restante en deux, puis une des sous-zones est recoupée en deux par le trait jaune. Si vous regardez l'arbre à droite, j'ai mis un carré bleu sous le carré vert, et un carré jaune sous le trait bleu.
Voici comment est codée ceci en C :
struct Axe
{
Point A,B;
};
struct BSP2D
{
Axe decoupe;
BSP2D* fils[2];
Segment* tableau;
int nbsegs;
}À l'instar du quadtree, seulement les feuilles contiendront la liste des segments correspondant à leur zone.
Les nœuds intermédiaires, eux, contiendront une droite de coupe (celle que j'ai mise en vert, bleu, jaune, violet sur le dessin).
L'idée de l'arbre BSP est couper en deux une zone pour en faire deux zones. Cette coupe n'est pas alignée sur les axes X ou Y comme la grille ou le Quadtree, elle est quelconque.
VI-B. Comment choisir les axes de coupe ?▲
Si le découpage est quelconque, ça ne veut pas dire qu'il est fait au hasard.
En effet, les axes de découpage sont astucieusement placés.
Le but est d'avoir à peu près le même nombre de segments d'un côté ou de l'autre, pour faire un arbre équilibré.
L'inconvénient du quadtree disparaît avec le BSP. Un arbre BSP est un arbre équilibré, même dans les cas où notre monde comporte beaucoup de murs à un endroit, et peu ailleurs, contrairement au quadtree.
Cependant, construire un tel arbre BSP est quelque chose de long. En effet, étant donné une soupe de segments, il faut trouver la droite qui coupera le tout intelligemment en faisant un bon équilibre entre les deux zones ainsi coupées.
Les algorithmes employés pour ça sont complexes, lourds et calculatoires.
C'est pour cela que le calcul d'un arbre BSP est quasiment toujours enregistré avec la carte du monde. C'est l'éditeur de carte qui va construire le BSP, et le sauvegarder.
Le joueur, quand il va lancer son jeu et charger sa carte, chargera le BSP tout fait avec.
VI-C. Calcul des collisions▲
Tout comme le quadtree, calculer les collisions dans un BSP revient à trouver, pour notre segment de déplacement, dans quelle(s) zone(s) il passe, et de tester ensuite les listes de segments des zones concernées.
Il faut donc, pour un point donné, descendre dans l'arbre BSP et se laisser guider vers la bonne feuille.
VI-C-1. Choisir la bonne zone▲
Si vous êtes sur un nœud, avec un point P, et que vous voulez savoir si votre point P est dans la zone du fils gauche, ou du fils droit, il vous suffit de faire un petit calcul.
Chaque axe est une droite orientée de A vers B.
Si on considère un point P, est-il à gauche de cette droite (on ira dans le fils gauche), ou à droite (on ira dans le fils droit).
Si vous avez bien lu le chapitre sur les collisions segment-segment, un simple calcul de déterminant fait l'affaire.
kitxmlcodelatexdvpd = \det(\vec{AB},\vec{AP}) = AB_x*AP_y-AB_y*AP_xfinkitxmlcodelatexdvp- Si d > 0, alors P est à gauche.
- Si d < 0 alors P est à droite.
- Si d == 0, on est sur un cas limite, on pourra ranger à gauche ou à droite, au choix, mais il est préférable de se tenir à son choix.
Le jeu vidéo Doom utilisait un BSP 2D.
Tous ces algorithmes ont leur équivalent en 3D. Je les présenterai donc dans la rubrique 3D.
Navigation▲
| Tutoriel précédent : gestion des décors | Sommaire | Tutoriel suivant : sprites enrichis |