Navigation▲
| Tutoriel précédent : chargement d'un monde, et la plus basique des caméras | Sommaire | Tutoriel suivant : lumière ponctuelle |
II. Introduction▲
Bienvenue dans mon onzième tutoriel de la série sur WebGL, le second qui n'est pas basé sur les tutoriels OpenGL de NeHe. Dans celui-ci, nous allons faire une sphère texturée avec éclairage directionnel, que le spectateur pourra faire tourner avec la souris.
Voici à quoi ressemble la leçon lorsqu'elle est exécutée sur un navigateur qui prend en charge WebGL :
Cliquez pour lire la vidéo
Cliquez ici pour voir la version live WebGL si vous avez un navigateur qui la prend en charge ; voici comment en obtenir un si vous n'en avez pas. Vous allez apercevoir momentanément une sphère blanche le temps de chargement de la texture, puis une fois chargée la lune avec de l'éclairage venant d'en haut à droite dirigée vers vous. Si vous la faites glisser, elle va tourner, la lumière restant inchangée. Si vous souhaitez changer l'éclairage, il y a des champs en dessous du canvas WebGL qui sembleront familiers à ceux de la septième leçon.
Plus de détails sur comment tout cela fonctionne ci-dessous…
Ces leçons sont destinées aux personnes ayant de bonnes connaissances en programmation, mais sans réelle expérience dans la 3D, le but est de vous donner les moyens de démarrer, avec une bonne compréhension de ce qui se passe dans le code, afin que vous puissiez commencer à produire vos propres pages Web 3D aussi rapidement que possible. Si vous n'avez pas lu les tutoriels précédents, vous devriez le faire avant de lire celui-ci. Je n'expliquerai ici que les nouveaux éléments. Cette leçon est basée sur la septième leçon, assurez-vous donc de l'avoir comprise (postez-y un commentaire si vous ne comprenez pas quelque chose).
Il y a deux façons d'obtenir le code de cet exemple, il suffit d'« Afficher la source » pendant que vous visionnez la version live, ou si vous utilisez GitHub, vous pouvez le cloner (ainsi que les autres leçons) à partir du dépôt.
Comme d'habitude, le meilleur moyen de comprendre le code de cette page est en commençant par la fin et de remonter tout en regardant les nouveautés. Le code HTML à l'intérieur des balises <body> n'est pas différent de la septième leçon, nous allons donc démarrer par le nouveau code situé dans webGLStart :
function webGLStart() {
canvas = document.getElementById("lesson11-canvas");
initGL(canvas);
initShaders();
initBuffers();
initTexture();
gl.clearColor(0.0, 0.0, 0.0, 1.0);
gl.enable(gl.DEPTH_TEST);
canvas.onmousedown = handleMouseDown; // NOUVEAU
document.onmouseup = handleMouseUp; // NOUVEAU
document.onmousemove = handleMouseMove; // NOUVEAU
tick();
}Ces trois nouvelles lignes nous permettent de détecter les évènements de la souris et faire ainsi tourner la lune lorsque l'utilisateur déplace sa souris. Il va de soi que nous voulons seulement capter les clics de la souris à l'intérieur du canvas 3D (car il serait gênant que la lune tourne alors que vous déplacez votre souris autre part dans la page HTML, par exemple dans les champs de texte de l'éclairage). Par contre, il est moins évidemment, mais nous souhaitons surveiller les évènements de relâchement de la souris sur le document plutôt que dans le canvas. En faisant cela, nous sommes en mesure de recueillir les évènements de déplacement même lorsque la souris est déplacée ou relâchée à l'extérieur du canvas 3D, à condition que le déplacement ait commencé à l'intérieur du canvas. Ceci nous empêche d'avoir une de ces pages irritantes où lorsque vous appuyez sur le bouton de la souris à l'intérieur de la scène que vous voulez tourner, et que vous relâchez le bouton à l'extérieur, la scène reste contrôlable lorsque vous repassez le curseur dans la scène. L'évènement de relâchement n'a pas été pris en compte : il pense toujours que vous faites glisser les choses jusqu'à ce que vous cliquiez quelque part.
En remontant un peu dans le code, nous arrivons à notre fonction tick qui, pour cette page, ne fait que préparer l'image suivante et appeler drawScene, car il n'a pas besoin de gérer les touches (parce que nous ne nous en préoccupons plus) ou d'animer la scène (car la scène ne répond qu'aux actions de l'utilisateur et ne fait pas d'animation indépendante).
function tick() {
requestAnimFrame(tick);
drawScene();
}Les prochaines modifications pertinentes sont dans la fonction drawScene. Nous commençons par les codes d'effacement du canvas et de perspective, puis faisons la même chose que dans la septième leçon pour mettre en place l'éclairage :
function drawScene() {
gl.viewport(0, 0, gl.viewportWidth, gl.viewportHeight);
gl.clear(gl.COLOR_BUFFER_BIT | gl.DEPTH_BUFFER_BIT);
mat4.perspective(45, gl.viewportWidth / gl.viewportHeight, 0.1, 100.0, pMatrix);
var lighting = document.getElementById("lighting").checked;
gl.uniform1i(shaderProgram.useLightingUniform, lighting);
if (lighting) {
gl.uniform3f(
shaderProgram.ambientColorUniform,
parseFloat(document.getElementById("ambientR").value),
parseFloat(document.getElementById("ambientG").value),
parseFloat(document.getElementById("ambientB").value)
);
var lightingDirection = [
parseFloat(document.getElementById("lightDirectionX").value),
parseFloat(document.getElementById("lightDirectionY").value),
parseFloat(document.getElementById("lightDirectionZ").value)
];
var adjustedLD = vec3.create();
vec3.normalize(lightingDirection, adjustedLD);
vec3.scale(adjustedLD, -1);
gl.uniform3fv(shaderProgram.lightingDirectionUniform, adjustedLD);
gl.uniform3f(
shaderProgram.directionalColorUniform,
parseFloat(document.getElementById("directionalR").value),
parseFloat(document.getElementById("directionalG").value),
parseFloat(document.getElementById("directionalB").value)
);
}Puis nous nous déplaçons à la position où nous souhaitons dessiner la lune.
mat4.identity(mvMatrix);
mat4.translate(mvMatrix, [0, 0, -6]);… Et voici le premier bout qui peut paraître étrange ! Pour des raisons que j'expliquerai un peu plus tard, nous stockons la rotation actuelle de la lune dans une matrice. Cette matrice commence à l'état de matrice identité (c'est-à-dire, aucune rotation), puis au fur et à mesure que l'utilisateur bouge la souris, elle change pour refléter ces manipulations. Donc, avant de dessiner la lune, nous devons appliquer cette matrice de rotation à la matrice modèle-vue actuelle, chose faite avec la fonction mat4.multiply :
mat4.multiply(mvMatrix, moonRotationMatrix);Une fois ceci fait, il reste à dessiner la lune. Ce code est assez standard, nous appliquons la texture et utilisons le même genre de code déjà employé de nombreuses fois pour indiquer à WebGL d'utiliser des tampons prêts à l'emploi pour dessiner un groupe de triangles :
gl.activeTexture(gl.TEXTURE0);
gl.bindTexture(gl.TEXTURE_2D, moonTexture);
gl.uniform1i(shaderProgram.samplerUniform, 0);
gl.bindBuffer(gl.ARRAY_BUFFER, moonVertexPositionBuffer);
gl.vertexAttribPointer(shaderProgram.vertexPositionAttribute, moonVertexPositionBuffer.itemSize, gl.FLOAT, false, 0, 0);
gl.bindBuffer(gl.ARRAY_BUFFER, moonVertexTextureCoordBuffer);
gl.vertexAttribPointer(shaderProgram.textureCoordAttribute, moonVertexTextureCoordBuffer.itemSize, gl.FLOAT, false, 0, 0);
gl.bindBuffer(gl.ARRAY_BUFFER, moonVertexNormalBuffer);
gl.vertexAttribPointer(shaderProgram.vertexNormalAttribute, moonVertexNormalBuffer.itemSize, gl.FLOAT, false, 0, 0);
gl.bindBuffer(gl.ELEMENT_ARRAY_BUFFER, moonVertexIndexBuffer);
setMatrixUniforms();
gl.drawElements(gl.TRIANGLES, moonVertexIndexBuffer.numItems, gl.UNSIGNED_SHORT, 0);
}Alors, comment faisons-nous pour créer les positions des vertex, les normales, les coordonnées de texture et tampons d'index avec les bonnes valeurs servant à dessiner une sphère ? C'est ce à quoi sert la nouvelle fonction : initBuffers.
Elle commence par définir les variables globales pour les tampons, fixer le nombre de bandes de latitude et de longitude à utiliser, ainsi que son rayon. Si vous deviez utiliser ce code dans une page WebGL de votre choix, vous devriez paramétrer le rayon et les bandes de latitude et longitude et stocker les tampons ailleurs que dans des variables globales. Je l'ai fait de cette façon simple afin de ne pas vous imposer une conception OO ou fonctionnelle particulière.
var moonVertexPositionBuffer;
var moonVertexNormalBuffer;
var moonVertexTextureCoordBuffer;
var moonVertexIndexBuffer;
function initBuffers() {
var latitudeBands = 30;
var longitudeBands = 30;
var radius = 2;Alors, que sont les bandes de latitude et de longitude ? Afin de dessiner un ensemble de triangles approximant une sphère, nous devons diviser cette dernière. Il y a plusieurs façons judicieuses de faire cela, et une manière simple basée sur la géométrie du collège qui (a) donne des résultats tout à fait convenables et (b) reste compréhensible sans faire mal à la tête. La voici donc. ![]() Elle est basée sur l'une des démonstrations du site de Khronos, qui fut initialement développée par l'équipe de WebKit, qui fonctionne comme suit.
Elle est basée sur l'une des démonstrations du site de Khronos, qui fut initialement développée par l'équipe de WebKit, qui fonctionne comme suit.
Commençons par fixer la terminologie : les lignes de latitude sont celles qui, sur un globe, vous disent à quelle distance du nord ou du sud vous vous trouvez. La distance les séparant, mesurée le long de la surface de la sphère, est constante. Si vous deviez découper une sphère de haut en bas le long de ses lignes de latitude, vous vous retrouveriez avec des morceaux en forme de lentille de contact pour le haut et le bas, et d'épaisses tranches en forme de disque vers milieu. (Si c'est difficile à visualiser, imaginez-vous couper une tomate en rondelles pour une salade, mais en essayant de garder sur toute la hauteur la même longueur de peau pour chaque tranche. Évidemment, les tranches vers le milieu seraient plus épaisses que celles du dessus.)
Les lignes de longitude sont différentes : elles divisent la sphère en segments. Si vous deviez couper une sphère selon ces lignes, cela ressemblerait plutôt à une orange.
Maintenant, pour dessiner notre sphère, imaginez que nous avons dessiné les lignes de latitude de haut en bas, et les lignes de longitude autour. Nous voulons déterminer tous les points où ces lignes s'entrecoupent : nos positions de vertex. On peut alors diviser chaque carré formé par deux lignes adjacentes de longitude et deux lignes adjacentes de latitude en deux triangles, et les dessiner. En espérant que l'image ci-dessous clarifie un peu plus les choses !

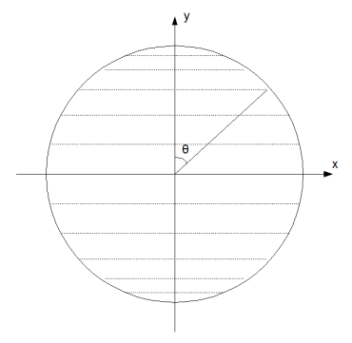
La prochaine question est de savoir comment on calcule ces points d'intersection. Supposons que la sphère ait un rayon d'une unité, et que nous commencions par prendre une tranche verticalement passant par son centre, dans le plan des axes X et Y, comme dans l'exemple ci-dessous.
De toute évidence, cette tranche a la forme d'un cercle et les lignes de latitude sont des lignes traversant ce cercle. Dans cet exemple, vous pouvez voir que nous nous concentrons sur la troisième bande de latitude à partir du haut, il y en a dix au total. L'angle entre l'axe Y et le point où la bande de latitude atteint le bord du cercle est ?. Avec un peu de trigonométrie, nous pouvons voir que le point a une coordonnée Y de cos(?) et une coordonnée X de sin(?).
Maintenant, généralisons ceci pour les points de toutes les lignes de latitude. Parce que nous souhaitons que chaque ligne soit séparée de sa voisine par la même distance le long de la surface de la sphère, nous pouvons simplement les définir par des valeurs de ? régulièrement espacées. Il y a ? radians dans un demi-cercle, nous pouvons donc dans notre exemple de dix lignes prendre des valeurs de ? de 0, ?/10, 2?/10, 3?/10, et ainsi de suite jusqu'à 10?/10, et être sûrs que nous avons divisé la sphère en égales bandes de latitude.
Maintenant, tous les points d'une latitude particulière, quelle que soit leur longitude, ont la même coordonnée Y. Donc, étant donné la formule pour la coordonnée Y ci-dessus, nous pouvons dire que tous les points autour de la énième latitude de la sphère de rayon unité et dix lignes de latitude auront la coordonnée Y cos(n?/10).
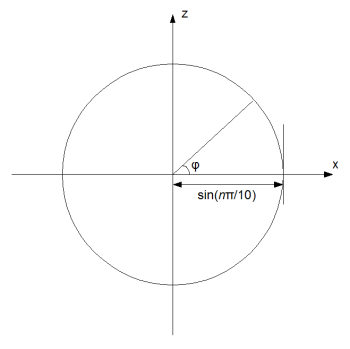
Nous avons réglé la coordonnée Y. Qu'en est-il de X et Z ? Eh bien, de la même façon que nous avons obtenu que la coordonnée Y était cos(n?/10), nous pouvons voir que la coordonnée X du point où Z est égal à zéro est sin(n?/10). Prenons une tranche différente de la sphère, comme montré dans l'image qui suit : une horizontale traversant le plan de la énième latitude.
Nous pouvons voir que tous les points sont dans un cercle de rayon de sin(n?/10) ; appelons cette valeur k. Si nous divisons le cercle en place par les lignes de longitude, que nous supposons au nombre de 10, et considérons que dans les 2? radians du cercle, l'angle ? prend les valeurs 0, 2?/10, 4?/10, et ainsi de suite. Nous pouvons une fois de plus avec la trigonométrie voir que notre coordonnée X est k.cos ? et notre coordonnée Z est k.sin ?.
Donc, pour généraliser, pour une sphère de rayon r, avec m bandes de latitude et n bandes de longitude, nous pouvons générer des valeurs pour x, y et z en prenant ? dans l'intervalle de 0 à ? divisé en m parties, et ? en divisant la plage de 0 à 2? en n parties, et en effectuant le calcul :
- x = r sin ? cos ?
- y = r cos ?
- z = r sin? sin ?
C'est ainsi que nous obtenons les vertex. Maintenant, qu'en est-il des autres valeurs dont nous avons besoin pour chaque point : les normales et les coordonnées de texture ? Eh bien, pour les normales c'est facile : rappelez-vous, une normale est un vecteur de longueur unité qui émerge directement d'une surface. Pour une sphère de rayon unité, c'est le même que le vecteur qui va du centre à la surface de la sphère - ce que nous avons déjà vu dans le cadre du calcul de la position du vertex ! En fait, la meilleure façon de calculer la position du vertex et la normale est d'appliquer les calculs ci-dessus sans effectuer la multiplication par le rayon, stocker les résultats des normales, puis de multiplier ces valeurs par le rayon pour obtenir les positions des vertex.
Les coordonnées de texture sont ici simples. Nous espérons que lorsque quelqu'un donne une texture à mettre sur une sphère, il nous donne une image rectangulaire (en effet, WebGL, pour ne pas dire JavaScript serait probablement embrouillé par quelque chose d'autre !). Sans risque, nous pouvons supposer que cette texture est étirée vers le haut et le bas selon la projection de Mercator. Cela signifie que nous pouvons diviser équitablement les coordonnées de texture u de la gauche vers la droite selon les lignes de longitude, de même les coordonnées v du haut vers le bas par les lignes de latitude.
OK, voici comment cela marche - le code JavaScript devrait maintenant être très facile à comprendre ! Nous parcourons toutes les tranches de latitude, et à l'intérieur de cette boucle, nous nous déplaçons à travers les segments longitudinaux, et nous générons les normales, les coordonnées de texture, et les positions des vertex pour chacun. La seule chose étrange à noter est que nos boucles se terminent lorsque l'indice est supérieur au nombre de lignes de longitude/latitude - à savoir, nous utilisons <= plutôt que < dans les conditions de boucle. Cela signifie que pour, disons 30 longitudes, nous allons générer 31 vertex par latitude. À cause de la périodicité des fonctions trigonométriques, le dernier sera à la même position que le premier, ce qui nous donne donc un chevauchement de sorte que tout se rejoint.
var vertexPositionData = [];
var normalData = [];
var textureCoordData = [];
for (var latNumber = 0; latNumber <= latitudeBands; latNumber++) {
var theta = latNumber * Math.PI / latitudeBands;
var sinTheta = Math.sin(theta);
var cosTheta = Math.cos(theta);
for (var longNumber = 0; longNumber <= longitudeBands; longNumber++) {
var phi = longNumber * 2 * Math.PI / longitudeBands;
var sinPhi = Math.sin(phi);
var cosPhi = Math.cos(phi);
var x = cosPhi * sinTheta;
var y = cosTheta;
var z = sinPhi * sinTheta;
var u = 1 - (longNumber / longitudeBands);
var v = 1 - (latNumber / latitudeBands);
normalData.push(x);
normalData.push(y);
normalData.push(z);
textureCoordData.push(u);
textureCoordData.push(v);
vertexPositionData.push(radius * x);
vertexPositionData.push(radius * y);
vertexPositionData.push(radius * z);
}
}Maintenant que nous avons les vertex, nous avons besoin de les assembler en générant une liste des indices des vertex contenant des séquences de six valeurs, chacune représentant un carré décomposé en une paire de triangles. Voici le code :
var indexData = [];
for (var latNumber = 0; latNumber < latitudeBands; latNumber++) {
for (var longNumber = 0; longNumber < longitudeBands; longNumber++) {
var first = (latNumber * (longitudeBands + 1)) + longNumber;
var second = first + longitudeBands + 1;
indexData.push(first);
indexData.push(second);
indexData.push(first + 1);
indexData.push(second);
indexData.push(second + 1);
indexData.push(first + 1);
}
}C'est en fait assez facile à comprendre. Nous bouclons à travers nos vertex, et pour chacun d'eux, nous stockons son indice dans first, puis cherchons longitudeBands + 1 indices plus loin pour trouver l'indice associé une bande de latitude plus bas - sans oublier le +1 à cause des vertex supplémentaires que nous avons dû ajouter pour permettre le chevauchement - et le stockons dans second. Nous générons ensuite deux triangles, comme sur le schéma suivant :
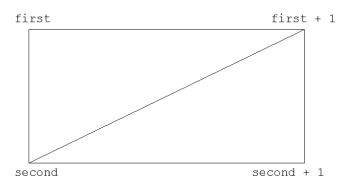
OK, la partie difficile est faite (au moins, la partie difficile à expliquer). Passons au code et observons les autres changements effectués.
Juste au-dessus de la fonction initBuffers, sont situées les trois fonctions qui gèrent la souris. Celles-ci méritent un examen attentif… Commençons par examiner attentivement ce que nous souhaitons faire. Nous voulons que le spectateur de notre scène puisse faire tourner la lune avec la souris. Une implémentation naïve pourrait être d'avoir, disons, trois variables représentant les rotations autour des axes X, Y et Z. Nous pourrions alors régler chacune de ces variables de manière appropriée lorsque l'utilisateur déplace la souris. Une rotation vers le haut ou vers le bas entraînerait un ajustement de la rotation autour de l'axe X et une rotation sur le côté, un ajustement autour de l'axe Y. Le problème avec cette manière de faire est que lorsque vous faites tourner un objet autour de plusieurs axes et que vous faites un certain nombre de rotations, l'ordre dans lequel vous les appliquez est important. Disons que le spectateur tourne la lune de 90° autour de l'axe Y, puis déplace la souris vers le bas. Si on effectue une rotation autour de l'axe X comme prévu, il verra la lune tourner autour de ce qui est maintenant l'axe Z, la première rotation a aussi fait tourner les axes. Cela lui paraîtra bizarre. Le problème ne fait que s'aggraver lorsque l'utilisateur effectue, disons, une rotation de 10 ° autour de l'axe X, puis 23 ° autour de l'axe Y, et puis… nous pourrions en toute logique dire quelque chose comme « étant donné l'état actuel de rotation, si l'utilisateur déplace la souris vers le bas, alors il faut ajuster les trois valeurs de la rotation de façon appropriée ». Mais un moyen plus facile de gérer ceci serait de garder une sorte de trace de chaque rotation que le spectateur a demandée à la lune, puis de les répéter à chaque fois que nous la dessinons. Cela peut sembler un moyen coûteux, à moins que vous vous rappeliez que nous avons déjà un très bon moyen de garder la trace d'une série de transformations géométriques en un seul lieu et place et de les appliquer en effectuant une seule opération : une matrice.
Nous gardons une matrice pour stocker l'état actuel de rotation de la lune, assez logiquement nommée moonRotationMatrix. Lorsque l'utilisateur déplace la souris, nous obtenons une série d'évènements de déplacement de la souris, et pour chacun nous déterminons le nombre de degrés de rotation autour des axes X et Y actuels observés par l'utilisateur. Nous calculons ensuite la matrice qui représente ces deux rotations, et la prémultiplions à la matrice moonRotationMatrix - « prémultiplions » pour la même raison que nous appliquons les transformations dans l'ordre inverse lors du positionnement de la caméra, la rotation se fait en termes d'espace caméra, pas d'espace modèle.
Donc, avec toutes ces explications, le code ci-dessous devrait être assez clair :
var mouseDown = false;
var lastMouseX = null;
var lastMouseY = null;
var moonRotationMatrix = mat4.create();
mat4.identity(moonRotationMatrix);
function handleMouseDown(event) {
mouseDown = true;
lastMouseX = event.clientX;
lastMouseY = event.clientY;
}
function handleMouseUp(event) {
mouseDown = false;
}
function handleMouseMove(event) {
if (!mouseDown) {
return;
}
var newX = event.clientX;
var newY = event.clientY;
var deltaX = newX - lastMouseX;
var newRotationMatrix = mat4.create();
mat4.identity(newRotationMatrix);
mat4.rotate(newRotationMatrix, degToRad(deltaX / 10), [0, 1, 0]);
var deltaY = newY - lastMouseY;
mat4.rotate(newRotationMatrix, degToRad(deltaY / 10), [1, 0, 0]);
mat4.multiply(newRotationMatrix, moonRotationMatrix, moonRotationMatrix);
lastMouseX = newX
lastMouseY = newY;
}C'est le dernier nouveau morceau important dans cette leçon. En remontant à partir de là, tous les changements que vous pourrez voir sont ceux nécessaires au code de texture, afin de charger la nouvelle texture dans les nouveaux noms de variables.
C'est tout ! Vous savez maintenant comment dessiner une sphère en utilisant un algorithme simple, mais efficace, et raccorder les évènements de souris pour permettre aux utilisateurs de manipuler vos objets 3D, et comment utiliser les matrices pour représenter l'état de rotation actuelle d'un objet dans une scène.
C'est tout pour maintenant, la leçon suivante vous montrera un nouveau type d'éclairage : l'éclairage ponctuel, qui vient d'un endroit particulier dans la scène et rayonne vers l'extérieur, tout comme la lumière d'une ampoule.
III. Remerciements▲
La texture de la lune vient du site JPL de la NASA. Le code utilisé pour générer la sphère est basé sur cette démonstration, initialement développée par l'équipe WebKit. Un grand merci à tous les deux !
Merci à LittleWhite pour sa relecture attentive et ClaudeLELOUP pour sa relecture orthographique.
Navigation▲
| Tutoriel précédent : chargement d'un monde, et la plus basique des caméras | Sommaire | Tutoriel suivant : lumière ponctuelle |